
Bewijs somregel sinus mbv parallellogram
Hoe bewijs ik de somregel van sinus mbv een rechthoek ABCD met daarin de parallellogram abcd en hoek Aad=x en hoek baB=y en hoek AdD=pi en hoek adc=x+y en ad=dc=1.
Herman
Leerling bovenbouw havo-vwo - woensdag 26 september 2007
Antwoord
Beste Herman,
Ik denk dat je hetvolgende bedoelt: zie tekening
Omdat ad=dc is je parallellogram een ruit.
Begrijp je waarom hoek adc=x+y?
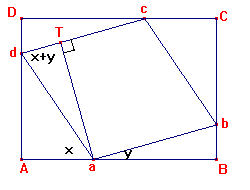
Kern van het bewijs:
Oppervlak van de ruit = sin(x+y).
Dat oppervlak kan je ook berekenen door het oppervlak van de driehoekjes af te trekken van dat van de rechthoek en je krijgt: sinx×cosy+cosx×siny.
De zijden ab, bc, cd en ad zijn allemaal 1.
Dan krijg je:
aT=sin(x+y)
Ad=sinx
Aa=cosx
dD=bB=siny
aB=cosy.
Oppervlak ruit= aT×ab=sin(x+y)
Oppervlak rechthoek= AD×AB=(sinx+siny)×(cosx+cosy)
Oppervlak driehoekjes=2x(oppervlak DAad+DaBb)=sinx×cosx+siny×cosy
Nu zelf de haakjes uitwerken en de driehoekjes van de rechthoek aftrekken en je hebt het bewijs!
Leuk hè! Ik kende hem zelf ook niet.
ldr
woensdag 26 september 2007
 ©2001-2024 WisFaq
©2001-2024 WisFaq
|