WisFaq!

Bewijs somregel sinus mbv parallellogram

Hoe bewijs ik de somregel van sinus mbv een rechthoek ABCD met daarin de parallellogram abcd en hoek Aad=x en hoek baB=y en hoek AdD=pi en hoek adc=x+y en ad=dc=1.

Herman
26-9-2007

Antwoord

Beste Herman,

Ik denk dat je hetvolgende bedoelt: zie tekening
Omdat ad=dc is je parallellogram een ruit.
Begrijp je waarom hoek adc=x+y?


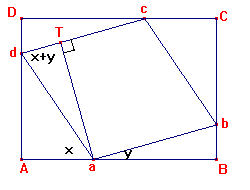
Kern van het bewijs:
Oppervlak van de ruit = sin(x+y).
Dat oppervlak kan je ook berekenen door het oppervlak van de driehoekjes af te trekken van dat van de rechthoek en je krijgt: sinx×cosy+cosx×siny.

De zijden ab, bc, cd en ad zijn allemaal 1.
Dan krijg je:
aT=sin(x+y)
Ad=sinx
Aa=cosx
dD=bB=siny
aB=cosy.

Oppervlak ruit= aT×ab=sin(x+y)
Oppervlak rechthoek= AD×AB=(sinx+siny)×(cosx+cosy)
Oppervlak driehoekjes=2x(oppervlak DAad+DaBb)=sinx×cosx+siny×cosy
Nu zelf de haakjes uitwerken en de driehoekjes van de rechthoek aftrekken en je hebt het bewijs!

Leuk hè! Ik kende hem zelf ook niet.

ldr
26-9-2007