Vergelijking met twee onbekenden

sorry ,wiskunde is maar voor mij tijdje geleden ,moet een klein programma schrijven maar ben echt vergeten hoe je onderstand vergelijking met twee onbekende kan oplossen
voorbeeld

(0.027+0.028)x+(0.025+0.024)y=0

of voorbeeld
(0.167+0.17)x+(0.096+0.095)y=0

wie weet voor jullie erg makkelijk maar voor mij ....
als je wilt svp met uitwerking

alvast hartelijk dank daarvoor
groetjes

marek
Ouder - donderdag 1 augustus 2002

Antwoord

Beste Marek,

Ik kan me voorstellen dat je je een beetje machteloos voelt bij het zien van een vergelijking met 2 variabelen als je wiskunde al een lange tijd niet meer hebt gebruikt. Daarom, zal ik even uitgebreid vertellen hoe het zit:

(0,027 + 0,028)x + (0,025 + 0,024)y = 0
Ik schrijf het even zo dat vind ik overzichtelijker:
x(0,027 + 0,028) + y(0,025 + 0,024) = 0
Je weet waarschijnlijk wel dat er eigenlijk dit staat:
x * (0,027 + 0,028) + y * (0,025 + 0,024) = 0

Zoals je weet, doe je eerst wat tussen haakjes staat. Dit ontstaat:

x * 0,055 + y * 0,049 = 0
Zoals je hopelijk nog wel herinnert, wordt dit:

0,055x + 0,049y = 0

Eén oplossing kun je nu al zien:
x=0 en y=0

Voor meer oplossingen zou ik het zo zien:
0,055x = -1 * 0,049y
Ik zal het even toelichten:

Omdat de uitkomst van de vergelijking 0,055x + 0,049y, 0 moet zijn, moet alles voor de + natuurlijk net zo groot zijn als alles na de +, maar dan negatief. Of datgene na de plus moet juist negatief zijn terwijl datgene voor de plus weer positief is. Dit is waarschijnlijk allemaal een beetje verwarrend. Ik geef even een voorbeeld, dan zul je het wel snappen:

0,055x + 0,049y = 0
Bijv.:
0,055x = -5
Dan moet dit ook waar zijn, anders is de uitkomst geen 0:
0,049y = 5
Of je zou het andersom kunnen stellen (dat 0,055x = 5 en 0,049y = -5).
0,055x en 0,049y hoeven niet per se met 5 en -5 vergeleken te worden, maar met welk getal dan ook (maakt echt niet uit welke, 4 en -4 kan bijv. ook).

We gaan verder met deze vergelijking:
0,055x = 5
x = 5 / 0,055 90,9
Nu doen we die andere:
0,049y = -5
y = -5 / 0,049 -102

Nu hebben we dus al een tweede oplossing gevonden:
x = 90,9 en y = -102

Even ter controle gaan we de waardes invullen in de oorspronkelijke formule:

(0,027 + 0,028)x + (0,025 + 0,024)y = 0
0,055 * 90,9 + 0,049 * -102 = 0,0015 0

Zoals je nu wel ziet, zijn er ongelooflijk veel oplossingen. Oneindig eigenlijk. Hierdoor kun je alle oplossingen in één grafiek laten zien. De formule hierbij is niet zo moeilijk te vinden. Maak gewoon een tabel :)

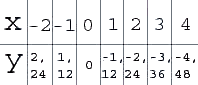Deze waarden vind je door een x-waarde te nemen, en daarvanuit de y berekenen.
De formule bij deze tabel (en dus bij de bijbehorende grafiek) is:

y = -1,12·x

Dit leid je af uit het feit dat bij elke x-stap (dus bij elke keer dat x met 1 wordt vergroot) de y-waarde met 1,12 verkleind wordt.
Als je de moeite neemt, dan kun je de grafiek erbij tekenen. Je ziet dan alle waarden die mogelijk zijn (binnen de stappen die je de assen geeft dan).

Ik hoop dat je het nu begrijpt,succes!

bk
donderdag 1 augustus 2002

©2001-2024 WisFaq