
Goniometrische vergelijkingen met machten
Ik kreeg in mijn boek de volgende vraag voorgeschoteld:
2·sin2(x) = 1
Hoe los ik dit op? Ik ben tot zover gekomen:
sin2(x) = ½
sin2(x) = (½ 2)2 2)2
sin2(x) = sin2(¼  ) )
x = ¼  + k·2 + k·2  v x = ¾ v x = ¾  + k·2 + k·2 
volgens het antwoordenboek moet er het volgende uitkomen:
x = ¼  + k·½ + k·½ 
Wat doe ik fout en hoe moet ik dit soort vergelijkingen dan wel oplossen? En hoe doe ik dan de volgende:
5·sin3(x) = 4
Heel erg bedankt,
Bart van der Vliet
Bart v
Iets anders - maandag 24 juni 2002
Antwoord
2sin2(x)=1Û
sin2(x)=1/2. deze stap is zowiezo goed.
verder weet je dat wanneer je een vergelijking hebt van de vorm:
x2=a, dat dan volgt:
x=+ a Ú x=- a Ú x=- a a
dus:
sin2(x)=1/2 Û
sin(x)=½ 2 Ú sin(x)=-½ 2 Ú sin(x)=-½ 2 2
Þ x=¼  +2k +2k  Ú x=¾ Ú x=¾  +2k +2k  (dit zijn de "plus"-oplossingen) Ú x=5/4 (dit zijn de "plus"-oplossingen) Ú x=5/4  + 2k + 2k  Ú x=7/4 Ú x=7/4  + 2k + 2k  (dit zijn de "min"-oplossingen) (dit zijn de "min"-oplossingen)
Op zich zijn deze oplossingen al okay. Maar laten we deze "zooi" eens even slim samenvatten.
Als je de hierbovengenoemde hoeken allemaal aanwijst op de eenheidscirkel, dan valt je direct op dat het hoeken zijn beginnend bij ¼  (ofwel 45°) en dan telkens een kwart cirkel (½ (ofwel 45°) en dan telkens een kwart cirkel (½  ) verderop weer eentje. ) verderop weer eentje.
Dit kun je samenvatten door te zeggen:
x = ¼  + ½k + ½k  , k=0,1,2,3,... , k=0,1,2,3,...
******************************************
Dan 5.sin3(x)=4 Û
sin3(x)=4/5 Û sin(x)=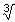 (4/5) (4/5)
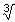 (4/5) is een of ander rot-getal, ook in de gonio. (4/5) is een of ander rot-getal, ook in de gonio.
Dit moet je met je rekenmachine verder uitwerken:
inv sin (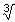 (4/5)) (4/5))
noem dit getal eventjes a
dan luidt de oplossing:
x= a + 2k  Ú x= Ú x=  -a + 2k -a + 2k 
vergeet die tweede oplossing niet!
suc6
Martijn
mg
maandag 24 juni 2002
 ©2001-2024 WisFaq
©2001-2024 WisFaq
|