
Oppervlakte van functies
Hoe bereken ik de positieve oppervlakte van deze figuur? Alvast bedankt voor jullie hulp, misschien kan ik voor mijn wiskunde er geraken dit jaar...
f(x) = x2 - 4x + 3
g(x) = x + 3
steven
Student Hoger Onderwijs BelgiŽ - woensdag 5 juni 2002
Antwoord
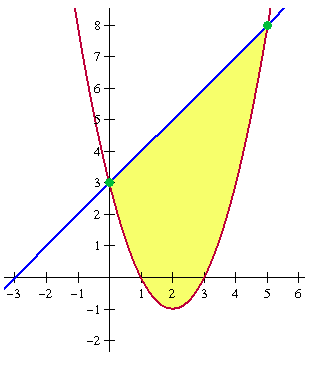
De snijpunten liggen in (0,3) en (5,8).
De oppervlakte tussen twee krommen is altijd gelijk aan de integraal van 'bovenste functie' minus 'onderste functie'.
De ligging t.o.v. de x-as is hierop niet van invloed!
$
\eqalign{
& \int\limits_0^5 {g(x) - f(x)\,\,dx} = \cr
& \int\limits_0^5 {x + 3 - (x^2 - 4x + 3)\,\,dx} = \cr
& \int\limits_0^5 { - x^2 + 5x\,\,dx} = \cr
& \left[ { - \frac{1}
{3}x^3 + 2\frac{1}
{3}x^2 } \right]_0^5 = \cr
& 20\frac{5}
{6} - 0 = \cr
& 20\frac{5}
{6} \cr}
$
MBL
woensdag 5 juni 2002
 ©2001-2024 WisFaq
©2001-2024 WisFaq
|