WisFaq!

Oppervlakte van functies

Hoe bereken ik de positieve oppervlakte van deze figuur? Alvast bedankt voor jullie hulp, misschien kan ik voor mijn wiskunde er geraken dit jaar...

f(x) = x² - 4x + 3
g(x) = x + 3

steven vanbelle
5-6-2002

Antwoord

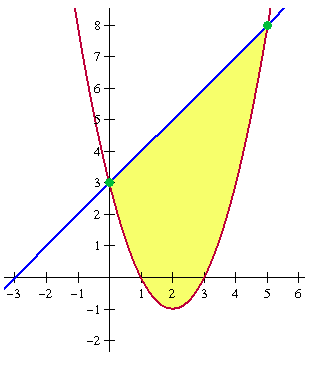
De snijpunten liggen in (0,3) en (5,8).

De oppervlakte tussen twee krommen is altijd gelijk aan de integraal van 'bovenste functie' minus 'onderste functie'.
De ligging t.o.v. de x-as is hierop niet van invloed!

$
\eqalign{
& \int\limits_0^5 {g(x) - f(x)\,\,dx} = \cr
& \int\limits_0^5 {x + 3 - (x^2 - 4x + 3)\,\,dx} = \cr
& \int\limits_0^5 { - x^2 + 5x\,\,dx} = \cr
& \left[ { - \frac{1}
{3}x^3 + 2\frac{1}
{3}x^2 } \right]_0^5 = \cr
& 20\frac{5}
{6} - 0 = \cr
& 20\frac{5}
{6} \cr}
$

MBL
5-6-2002