Ongelijkheden en snijpunten

Hallo,

Ik heb een probleem met de volgende vraag:

Gegeven is: f(x)=(2x-1)/(x+1)

Ik moet de snijpunten van deze hyperbool met de functie g(x)= 2x-3 uitrekenen, ik kom hier niet uit door de functies aan elkaar gelijk te stellen...

Verder weet ik ook niet helemaal hoe ik de volgende ongelijkheid op moet lossen: (2x-1)/(x+1)$<$2x-3
En wat voor oplossingen krijg ik als ik er absolute waarden van maak?: |(2x-1)/(x+1)|$<$|2x-3|

Kunnen jullie me helpen, heel erg bedankt

Marc H
Leerling bovenbouw havo-vwo - zaterdag 22 mei 2004

Antwoord

We doen nog een voorbeeld. We volgen daarbij het stappenplan van oplossen van ongelijkheden.

1.

$
\eqalign{
& \frac{{2x - 1}}
{{x + 1}} = 2x - 3 \cr
& (x + 1)(2x - 3) = 2x - 1 \cr
& 2x^2 - x - 3 = 2x - 1 \cr
& 2x^2 - 3x - 2 = 0 \cr
& x_{1,2} = \frac{{3 \pm \sqrt {( - 3)^2 - 4 \cdot 2 \cdot - 2} }}
{{2 \cdot 2}} = \frac{{3 \pm \sqrt {25} }}
{4} = \frac{{3 \pm 5}}
{4} \cr
& x = - \frac{1}
{2} \vee x = 2 \cr}
$

2.

Er is mogelijk een probleem bij $x=-1$. De grafiek van $f(x)=(2x-1)/(x+1)$ heeft een asymptoot $x=-1$.

3.



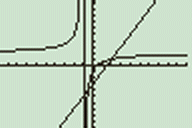
4.

$-1\lt x\lt$-¹/₂ of $x>24$

Het tweede gedeelte van je vraag kan je oplossen door de opgave te splitsen in twee delen:

1. $2x-3>0$
2. $2x-3<0$

In het eerste geval geldt alles wat je vindt alleen voor $x\geq$1¹/₂ en het tweede deel geldt alles alleen voor $x<-$1¹/₂. Maar verder precies als hierboven...

zaterdag 22 mei 2004

©2001-2024 WisFaq