WisFaq!

Ongelijkheden en snijpunten

Hallo,

Ik heb een probleem met de volgende vraag:

Gegeven is: f(x)=(2x-1)/(x+1)

Ik moet de snijpunten van deze hyperbool met de functie g(x)= 2x-3 uitrekenen, ik kom hier niet uit door de functies aan elkaar gelijk te stellen...

Verder weet ik ook niet helemaal hoe ik de volgende ongelijkheid op moet lossen: (2x-1)/(x+1)<2x-3
En wat voor oplossingen krijg ik als ik er absolute waarden van maak?: |(2x-1)/(x+1)|<|2x-3|

Kunnen jullie me helpen, heel erg bedankt

Marc Hilhorst
22-5-2004

Antwoord

We doen nog een voorbeeld. We volgen daarbij het stappenplan van oplossen van ongelijkheden.

1.

\eqalign{ & \frac{{2x - 1}} {{x + 1}} = 2x - 3 \cr & (x + 1)(2x - 3) = 2x - 1 \cr & 2x^2 - x - 3 = 2x - 1 \cr & 2x^2 - 3x - 2 = 0 \cr & x_{1,2} = \frac{{3 \pm \sqrt {( - 3)^2 - 4 \cdot 2 \cdot - 2} }} {{2 \cdot 2}} = \frac{{3 \pm \sqrt {25} }} {4} = \frac{{3 \pm 5}} {4} \cr & x = - \frac{1} {2} \vee x = 2 \cr}

2.

Er is mogelijk een probleem bij x=-1. De grafiek van f(x)=(2x-1)/(x+1) heeft een asymptoot x=-1.

3.



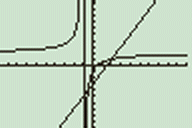
4.

-1\lt x\lt-¹/₂ of x>24

Het tweede gedeelte van je vraag kan je oplossen door de opgave te splitsen in twee delen:

1. 2x-3>0
2. 2x-3<0

In het eerste geval geldt alles wat je vindt alleen voor x\geq1¹/₂ en het tweede deel geldt alles alleen voor x<-1¹/₂. Maar verder precies als hierboven...

WvR
22-5-2004