Formule voor punten op een cirkel!

Stel we nemen n punten op de omtrek van een cirkel, en als we allemaal met elkaar verbinden, krijgen we allemaal snijpunten binnen de cirkel. Ook allemaal deellijnstukken en gebieden. Kent U een formule voor:
1 het aantal snijpunten 2 het aantal gebieden 3 het aantal deellijnstukken.
Ik heb al voor het aantal gebieden voor n= 1 t/m 5 getekend en gezien dat het een macht van 2 zou kunnen zijn voor de formule. Alleen bij n=6 klopt dit niet meer. Lastig.
Bij voorbaat dank.

Jack
Student hbo - zaterdag 24 april 2004

Antwoord

Hallo Jack,

Op het eerste gezicht lijkt jouw vraag op Circle Division by Lines, maar jouw probleem is net iets anders, omdat je ervan uitgaat dat je alle lijnen tussen de n punten tekent. Bij Circle Division by Lines moest je nog goed opletten hoe de lijnen precies georienteerd waren, maar nu is dat minder ingewikkeld. Wel ga ik er vanuit dat je de punten niet toevallig net zo gekozen hebt dat meerdere lijnen door één punt gaan (en eigenlijk is het daarmee toch weer hetzelfde als bij Circle Division by Lines, waar de uitzonderings-situatie evenwijdigheid van lijnen is).


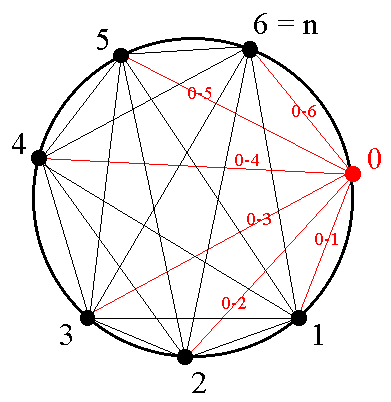
Je vraagstuk leent zich heel goed voor een aanpak met volledige inductie. Stel we hebben al een n-tal punten op een cirkel (in de tekening n=6). We noemen

• s(n) = het aantal snijpunten tussen de lijnen,
• g(n) = het aantal gebieden waarin de cirkel door de lijnen wordt verdeeld,
• l(n) = het aantal deellijnstukken van snijpunt tot snijpunt.

Nu zetten we er nog (n+1)^e punt bij. Wat gebeurt er dan met s,g en l? Zonder beperking van algemeenheid noemen we het nieuwe punt 0 en de rest {1,2,...,n} en we veronderstellen dat punt 0 tussen de punten 1 en n ligt en de overige punten op volgorde over de cirkel zijn verdeeld. De lijnen die er nu bij komen zijn 0-1, 0-2, ..., 0-i, ..., 0-n. Laten we per lijn die er bij komt kijken wat er verandert aan s,g en l:

Voor de eerste lijn 0-1 (en analoog voor 0-n):
Deze doorsnijdt geen enkele andere lijn dus D₁s = 0. Hij creëert wel één nieuw gebied, dus D₁g = +1. Bovendien is het natuurlijk één nieuw lijnstuk, dus D₁l = +1 (niet meer omdat hij geen andere lijnen snijdt).

Voor de tweede lijn 0-2 (en analoog voor 0-(n-1)):
Deze doorsnijdt alle lijnen komend uit punt 1, behalve die naar 2 (en die naar 0). Dat zijn er n-2, dus D₂s = +(n-2). Deze n-2 snijpunten op 0-2 verdelen de lijn 0-2 in n-1 lijnstukken die evenzoveel gebieden verdelen in twee gebieden, waarvan er dus één nieuw is. Dus D₂g = +(n-1). Het aantal lijnstukken dat er is bijgekomen is niet alleen de n-1 lijnstukken op 0-2, maar ook n-2 op de doorsneden lijnen, dus D₂l = (n-1)+(n-2).

Heb je het systeem al door? Dan gaan we het nu voor een willekeurige lijn 0-i met i tussen 1 en n doen (ga anders nog even verder met 0-3 en eventueel 0-4).

Voor de lijn 0-i (en analoog voor 0-(n-i+1)):
Deze doorsnijdt alle lijnen tussen de punten uit {1,..., i-1} en de punten uit {i+1,..., n}. Dat zijn er (i-1)·(n-i), dus D_is = (i-1)·(n-i). Deze (i-1)·(n-i) snijpunten verdelen de lijn 0-i in (i-1)·(n-i)+1 lijnstukken evenzoveel gebieden in tweeën delen, dus D_ig = (i-1)·(n-i)+1 = D_is + 1. Het aantal lijnstukken dat er is bijgekomen zijn de (i-1)·(n-i)+1 op 0-i en (i-1)·(n-i) op de doorsneden lijnen, dus D_il = (i-1)·(n-i) + 1 + (i-1)·(n-i) = 2 D_is + 1.

Als we nu willen weten hoeveel snijpunten, gebieden en lijnstukken erbij komen door het toevoegen van het (n+1)^e punt, dan hoeven we dit alleen nog maar te sommeren over i van 1 t/m n:
Ds = _i=1åⁿD_is = _i=1åⁿ(i-1)·(n-i) = _i=1åⁿ(-n+(n+1)i-i²) = -n² + (n+1)·¹/₂n(n+1) - ¹/₆ n(n+1)(2n+1) = ¹/₆n³ - ¹/₂n² + ¹/₃n = ¹/₆n(n-1)(n-2).
In de inductie-stap krijg je dus s(n+1) = s(n) + ¹/₆n(n-1)(n-2), dus s(n) = s(0) + _m=1å^n-1 (¹/₆m(m-1)(m-2)). Nu is het handig om te weten dat het sommeren over m van een polynoom in m met graad k, een polynoom van graad k+1 oplevert. Dus s(n) = a n⁴ + b n³ + c n² + d n + e. Je kunt nu a,b,c,d en e vinden door enkele waarden voor n in te vullen (handig trucje is overigens om ook n=-1 en n=-2 te gebruiken door gewoon s(n) = s(n+1)-Ds toe te passen). Het antwoord luidt:

s(n) = ¹/₂₄n⁴-¹/₄n³+¹¹/₂₄n²-¹/₄n = ¹/₂₄n(n-1)(n-2)(n-3).

Voor g en l kun je natuurlijk deze zelfde berekeningen opnieuw uitvoeren, maar het kan ook slimmer:

• Dg = _i=1åⁿD_ig = _i=1åⁿ(D_is + 1) = Ds + n,
• Dl = _i=1åⁿD_il = _i=1åⁿ(2 D_is + 1) = 2 Ds + n.

Hieruit volgt dat g(n) = s(n) + ¹/₂n(n-1) + g(0) en l(n) = 2 s(n) + ¹/₂n(n-1) + l(0), zodat:

• s(n) = ¹/₂₄n(n-1)(n-2)(n-3),
  
• g(n) = s(n) + ¹/₂n(n-1) + 1,
• l(n) = 2 s(n) + ¹/₂n(n-1).

Ik hoop je hiermee geholpen te hebben,

Guido Terra

Zie Wat te bewijzen is - Martin Kindt

gt
woensdag 28 april 2004

Re: Formule voor punten op een cirkel!

©2001-2024 WisFaq