
Re: Betrouwbaarheid percentages
Alvast bedankt voor de snelle reactie. Alleen zijn nog niet al m'n vragen beantwoord. Ik heb namelijk het aantal onderzochte leerlingen dat op een bepaalde manier telt als percentage van het totaal aantal onderzochte leerlingen genomen. Sommige percentages schelen maar iets van 5 a 10%. Wat kan ik daar over zeggen? Kan ik zeggen dat er echt een verschil, dat er meer mensen op de ene dan op de andere manier tellen, of moet er een groter verschil zijn? En hoe groot moet dat verschil zijn? Is het ook nog zo dat een verschil van 10% bij een combinatie van 10% op manier 1 en 20% op manier 2 anders behandeld moet worden dan een verschil van 10% bij een combinatie van 30% op manier 3 en 40% op manier 4, omdat in het laatste geval het verschil relatief kleiner is?
Leny v
Leerling bovenbouw havo-vwo - zaterdag 6 december 2003
Antwoord
Een manier die zeker niet helemaal correct is:
telmethode 3: 5 van de 104 = 4,80%
telmethode 5: 12 van de 104 = 11,54%
Is dit verschil nu significant of kan het aan het toeval liggen ?
Een manier waarop je daar in ieder geval iets over kunt zeggen is het maken van een betrouwbaarheidsinterval voor de werkelijke fractie bij telmethode 3 en bij telmethode 5.
De formule hiervan is:
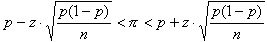
Die z waarde komt uit de gekozen betrouwbaarheid, bij 95% is dit 1,96.
Wanneer je voor telmethode 3 deze formule invult krijg je:
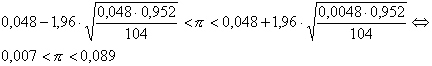
Die p is hierin de werkelijke, maar onbekende fractie, van mensen in de hele populatie die op deze manier tellen.
Voor telmethode 5 krijg je analoog:
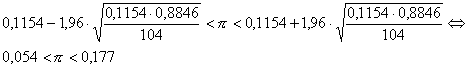
Omdat deze betrouwbaarheidsintervallen elkaar overlappen is er in werkelijkheid geen verschil tussen de beide telmethoden aan te tonen.
Nu kun je tegen deze aanpak van alles inbrengen: dat het geen toets is, dat je met een toets wat scherper kunt toetsen, dat je bij dergelijke kleine percentages geen normale verdeling zou moeten gebruiken. Allemaal waar. Maar als je een echte verschiltoets voor fracties zou uitvoeren is ook dat niet toegestaan omdat beide telmethoden als percentages van één totaal gegeven zijn. Derhalve is aan de voorwaarde van onafhankelijkheid tussen beide uitkomsten niet voldaan.
In feite komt het er uiteindelijk op neer dat je steekproef te klein is om verschil tussen het gebruik van telmethoden 3 en 5 echt aan te tonen.
Met vriendelijke groet
JaDeX

donderdag 11 december 2003
 ©2001-2024 WisFaq
©2001-2024 WisFaq
|