
Differentieren en limiet berekenen
Hoi wisfaq,
Kunt u mij helpen bij de volgende opgaven:
f(x)= lnx/(2-lnx) hiervan moet ik de afgeleide bepalen dan krijg ik volgens de quotientregel als eindantwoord;
f'(x)= 2/(2-lnx)2 maar het antwoordenboek drukt bij de noemer nog een x:
f'(x)= 2/(x(2-lnx))2 maar waar komt die x dan vandaan ?
Dan had ik nog een vraag over dit:
2) lim¯0 sinx.(0.5)logx (0.5 is de grondtal,dus geen vermenigvuldiging)
Hoe bewijst men dat deze limiet als uitkomst 0 heeft ?
Bijvoorbaat dank voor u antwoord.
Zafarp
Leerling bovenbouw havo-vwo - woensdag 9 juli 2003
Antwoord
Hoi,
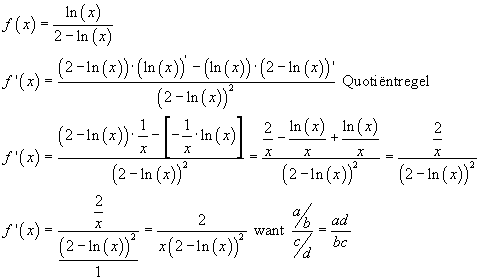
Om nu de rechterlimiet te berekenen zou ik een tabelletje maken waarbij de x steeds dichter naar 0 gaat, en hieruit de limiet (¹ functiewaarde) bepalen.
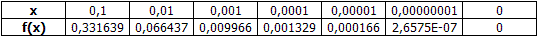
De dalende x-waarden geven aan dat je van rechts komt, en als x = 0, wordt met f(x) de rechterlimiet voor x gaande naar 0 bedoeld, want functiewaarde is hier niet gedefinieerd. Het kan ook op 'n andere manier, maar dan moet je bekend zijn met de Stelling van L'Hopital (en ik betwijfel of dat het geval is...).
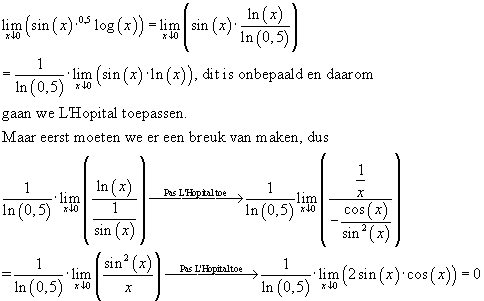
Die laatste twee 1/ln(0,5) moeten trouwens -1/ln(0,5) zijn.
Groetjes,
Davy.

donderdag 10 juli 2003
 ©2001-2024 WisFaq
©2001-2024 WisFaq
|