De bissectrice en de overstaande zijde

Hoe bewijs ik dat: de bissectrice van een hoek van een driehoek de overstaande zijde verdeelt in stukken die zich verhouden als de aanliggende zijden?

Eva
Student Hoger Onderwijs België - zaterdag 24 mei 2003

Antwoord

Noem de driehoek ABC. AD is de bissectrice van de hoek BAC zodat de hoeken BAD en DAC gelijk zijn. Neem op het verlengde van AD een punt E zodat |AC|=|CE|. De hoeken DAC en DEC zijn nu gelijk, omdat de driehoek ACE gelijkbenig is.



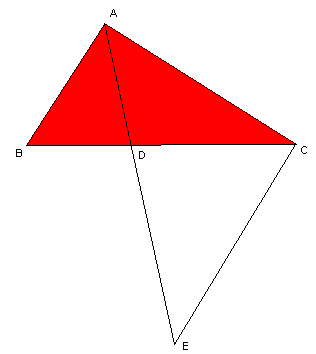
De driehoeken ABD en ECD zijn nu gelijkvormig omdat ze twee hoeken gelijk hebben, namelijk

BDA = CDE (overstaande hoeken)
BAD = DEC (want ze zijn beide gelijk aan DAC)

Uit die gelijkvormigheid volgt dan dat

|BD|/|AB| = |CD|/|CE|

Met |AC|=|CE| wordt dat

|BD|/|AB| = |CD|/|AC| of
|BD|/|CD| = |AB|/|AC|

zaterdag 24 mei 2003

©2001-2024 WisFaq