WisFaq!

De bissectrice en de overstaande zijde

Hoe bewijs ik dat: de bissectrice van een hoek van een driehoek de overstaande zijde verdeelt in stukken die zich verhouden als de aanliggende zijden?

Eva
24-5-2003

Antwoord

Noem de driehoek ABC. AD is de bissectrice van de hoek BAC zodat de hoeken BAD en DAC gelijk zijn. Neem op het verlengde van AD een punt E zodat |AC|=|CE|. De hoeken DAC en DEC zijn nu gelijk, omdat de driehoek ACE gelijkbenig is.



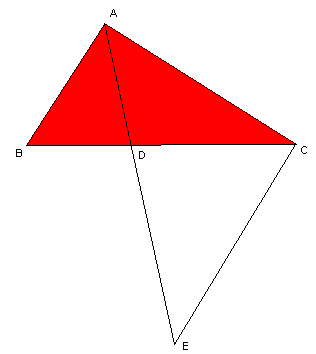
De driehoeken ABD en ECD zijn nu gelijkvormig omdat ze twee hoeken gelijk hebben, namelijk

BDA = CDE (overstaande hoeken)
BAD = DEC (want ze zijn beide gelijk aan DAC)

Uit die gelijkvormigheid volgt dan dat

|BD|/|AB| = |CD|/|CE|

Met |AC|=|CE| wordt dat

|BD|/|AB| = |CD|/|AC| of
|BD|/|CD| = |AB|/|AC|

cl
24-5-2003