|
|
|
\require{AMSmath}
Re: Kwadratisch vraagstuk
beste
ik snap er helemaal niets van.
Waarom wilt u β zoeken als die gegeven is namelijk 0.75?
Hoe weet u dat het punt 0.9 of-0.9 dat je daar op 48(wat 0.48 moet zijn) zal komen. Je hebt geen nulpunten dus kun je toch niet weten dat de parabool in dat punt komt?
maxime
2de graad ASO - dinsdag 28 maart 2023
Antwoord
Ik heb de $\beta$ expliciet `uitgerekend' om de oplossing volledig te maken.
Ik ben het met je eens dat die al gegeven is, maar het is ook voor de andere lezers.
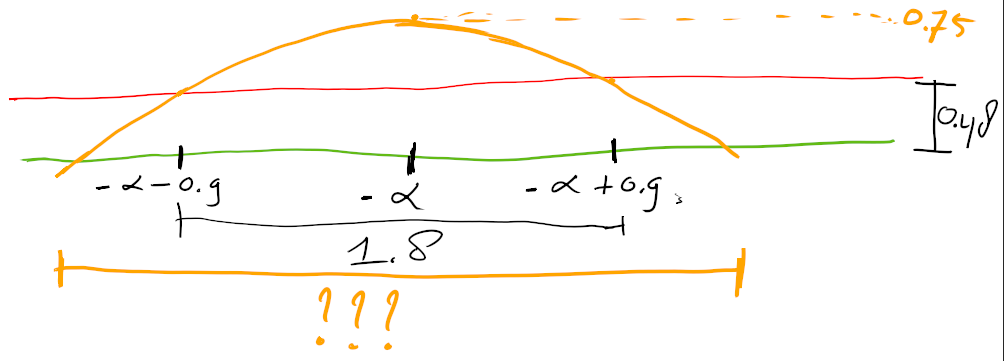
In het plaatje nemen we voor het gemak $\alpha=0$. Die afstand van $1.8\,\mathrm{m}$ heb ik verdeeld in $0.9\,\mathrm{m}$ links en $0.9\,\mathrm{m}$ rechts van $-\alpha$. Op die plekken is de kangoeroe precies $0.48\,\mathrm{m}$ hoog, vandaar $f(0.9)=f(-0.9)=0.48$.
Dat geeft $a\cdot0.9^2+0.75=0.48$, en dus $a=-\frac{0.27}{0.81}=-\frac13$.
Nu nog
$$-\frac13x^2+\frac34=0
$$oplossen voor de lengte van de sprong.
kphart
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 29 maart 2023
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 97657