Ik ben het met je eens dat die al gegeven is, maar het is ook voor de andere lezers.
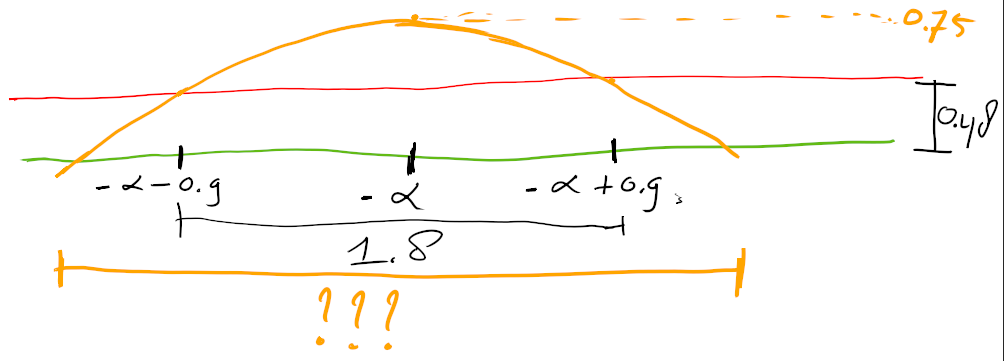
In het plaatje nemen we voor het gemak $\alpha=0$. Die afstand van $1.8\,\mathrm{m}$ heb ik verdeeld in $0.9\,\mathrm{m}$ links en $0.9\,\mathrm{m}$ rechts van $-\alpha$. Op die plekken is de kangoeroe precies $0.48\,\mathrm{m}$ hoog, vandaar $f(0.9)=f(-0.9)=0.48$.
Dat geeft $a\cdot0.9^2+0.75=0.48$, en dus $a=-\frac{0.27}{0.81}=-\frac13$.
Nu nog
$$-\frac13x^2+\frac34=0
$$oplossen voor de lengte van de sprong.
kphart
29-3-2023