|
|
|
\require{AMSmath}
Re: De som van de leeftijden
4x = 40
x = 10
Dus ik ga er van uit dat ik toen 10 jaar was. maar u was toen ook 10 jaar en nu bent u nog steeds 10 jaar. Wat was destijds de som van onze leeftijden?
Als hij nu 40 is en destijds 10 dan moet je 30 jaar terug.
Dus moet je (40-30)+(10-30) = 10 + (-20) = -10
Maar ik weet niet of ik juist bezig ben want -10 is een raar getal. Ik begrijp niet goed hoe ik verder moet.
tuur
3de graad ASO - woensdag 2 december 2020
Antwoord
Dat kan niet goed zijn. Je vergelijking klopt niet want de leeftijd van 'ik' is 'nu' niet gelijk aan $4x$.
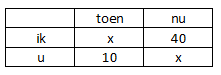
Neem 's aan dat $x=20$, dan is 'ik' 10 jaar ouder dan 'u' en dan zou 'u' nu 30 jaar moeten zijn. Dat klopt ook niet, maar 't zou hebben gekund...
Het verschil in leeftijd tussen 'ik' en 'u blijft gelijk als je van 'toen' naar 'nu' gaat. Dat betekent:
$x-10=40-x$
Oplossen geeft je de oplossing!
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 2 december 2020
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 91046