|
|
|
\require{AMSmath}



Re: Er zijn twee driehoeken ABC Welke?
Bedankt! Is er ook een manier om dit te doen met de sinusregel?
Mario
Leerling bovenbouw havo-vwo - zondag 14 mei 2017
Antwoord
Ja dat kan zeker. Dat gaat zo:
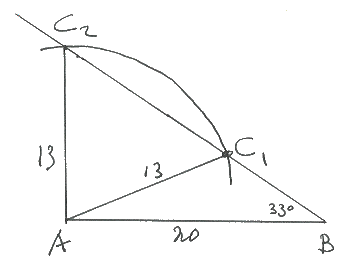
$
\eqalign{
& \frac{{13}}
{{\sin 33^\circ }} = \frac{{20}}
{{\sin \angle C}} \cr
& \sin \angle C = \frac{{20 \cdot \sin 33^\circ }}
{{13}} \approx 0,838 \cr
& \angle C_2 \approx 57^\circ \,\,en\,\,\angle C_1 \approx 123^\circ \cr
& \frac{{13}}
{{\sin 33^\circ }} = \frac{{BC_2 }}
{{\sin 90^\circ }} \cr
& BC_2 = \frac{{13 \cdot \sin 90^\circ }}
{{\sin 33^\circ }} \approx 23,87 \cr
& \frac{{13}}
{{\sin 33^\circ }} = \frac{{BC_1 }}
{{\sin 24^\circ }} \cr
& BC_1 = \frac{{13 \cdot \sin 24^\circ }}
{{\sin 33^\circ }} \approx 9,71 \cr}
$
Dat kan ook. 't Is wel handig want dit kan dan zonder GR maar bijvoorbeeld met een gewone rekenmachine.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 15 mei 2017
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Dit is een reactie op vraag 84415
Dit is een reactie op vraag 84415 

