|
|
|
\require{AMSmath}



Re: Bewijs driehoek gelijkbenig cirkels
hmm oke.
Volgens mij hebben ze  ACP en ACP en  ABC gemeenschappelijk, omdat dit te maken heeft met de omtrekshoek volgens mij. ABC gemeenschappelijk, omdat dit te maken heeft met de omtrekshoek volgens mij.  B hoort bij boog AC. Maar ik zie niets wat bij B hoort bij boog AC. Maar ik zie niets wat bij  ACP kan horen... ACP kan horen...
en hoe ik er mee verder moet.
Omdat  p= p= p en p en  PBC= PBC= PCA moet hoek PCA moet hoek  PAC gelijk zijn aan hoek PAC gelijk zijn aan hoek  PCB toch? PCB toch?
Richar
Leerling bovenbouw havo-vwo - dinsdag 27 maart 2012
Antwoord
Dag Richard,
Inderdaad zijn de hoeken ACP en ABC aan elkaar gelijk.
Niet alleen is ÐABC = ÐB = 1/2bg(AC), maar dit is ook het geval met ÐACP. Bewijs? Zie hierna.
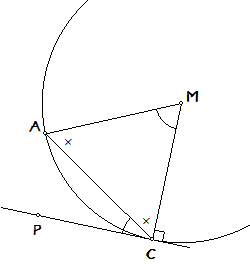
In bovenstaande figuur is:
ÐM = bg(AC) ; middelpuntshoek
ÐACP = 90° - ÐACM = 90° - x
ÐACP = 1/2(180° - 2x) = 1/2ÐM
Dus:
ÐACP = 1/2bg(AC)
De hoek ACP is dus eveneens een omtrekshoek (een hoek tussen een koorde en een raaklijn in een eindpunt van die koorde).
En dan zijn de driehoeken PAC en PCB uit je oorsponkelijke probleem inderdaad gelijkvormig!

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 27 maart 2012
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|








 Dit is een reactie op vraag 67235
Dit is een reactie op vraag 67235  ACP en
ACP en 

