|
|
|
\require{AMSmath}
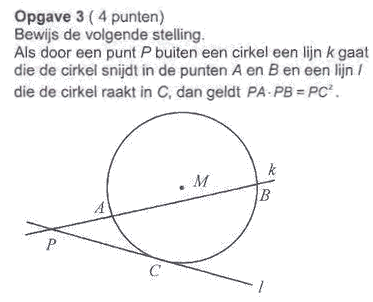
Bewijs driehoek gelijkbenig cirkels
Ik zit met een probleem, ik zie de eerste stap in het bewijs niet.
De stelling heb ik allereerst maar eens anders geschreven: PA·PB=PC·PC
Is er iemand die me wat tips kan geven?
Richar
Leerling bovenbouw havo-vwo - maandag 26 maart 2012
Antwoord
Dag Richard,
Die relatie kan je op nog andere manier schrijven: PA/PC = PC/PB.
En dat 'riekt' naar gelijkvormigheid van driehoeken...
PA & PC zijn zijden van driehoek PAC en PC & PB zijn zijden van driehoek PBC.
En, die driehoeken hebben hoek P gemeenschappelijk!
Hebben ze nog een tweede gemeenschappelijke hoek?
Teken eens de lijnstukken AC en BC.
En denk vervolgens aan omtrekshoeken en bogen (die cirkel moet je immers ook gebruiken...).
En betrek daarbij natuurlijk ook het raken van de lijn l. Ook dat gegeven kan je in verband brengen met een omtrekshoek (waarom is hoek ACP gelijk aan hoek ABC?).
Succes!
PS. Het 'gelijkbenig' in de kop van de vraag (MA = MB?) is dus niet van toepassing.
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 27 maart 2012
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Re: Bewijs driehoek gelijkbenig cirkels