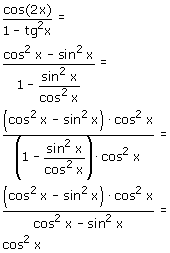WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

cos(2x)/(1-tan²x) = cos²x

Hallo,

tijdens de voorbereidingen op mijn examen kwam ik op dit :
cos(2x)/(1-tan²x) = cos²x
leek me gemakkelijk, maareuh.... 'k kan 'm momenteel niet oplossen :-(
ik heb het al op drie verschillende manieren geprobeerd :
ll = cos2x/(1-tan²x)
<=>(cos²x - sin²x)/1-(sin²x/cos²x)
maar dan zie 'k al geen uitweg meer
tweede manier :
ll = cos2x/(1-tan²x)
<=> ((1-2sin²c-1)/(1-sin²x)) * 1/cos²x
meuh... lukt ook niet en bij de derde manier met cos2x = 2cos²x-1 heb 'k een gigantische omweg ...
Vincen
3de graad ASO - zaterdag 30 november 2002

Antwoord

Hoi,

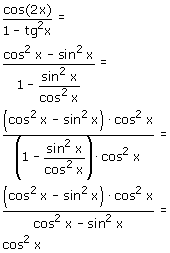
Het gaat hier wel degelijk om een identiteit en niet om een vergelijking...

Groetjes,
Johan

andros

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 30 november 2002