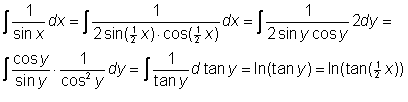|
|
|
\require{AMSmath}



Re: Re: Een deel van de oppervlakte van een cirkel
Okey hartelijk dank,
Ik wil toch wel graag weten hoe die integraal van 1/cos(x) gevonden word en ik ga de rest zelf proberen en als ik er niet uit kom dan stuur ik weer een reactie.
Met vriendelijke groet,
Bob
Bob
Student hbo - zondag 10 augustus 2008
Antwoord
Beste Bob,
Eerst even de primitieve van 1/sinx, die is nl. wat makkelijker.
Dan zullen we x vervangen door p/2-y, zodat cosx=siny.
1)Vervang sinx door 2sin(1/2x)cos(1/2x)
2)vervang x door 2y
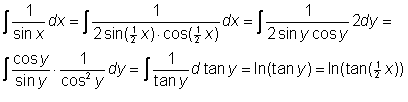
Nu ò1/cosx dx:
Nu gebruiken we de substitutie x=p/2-y (of y/2=p/4-x/2) en dus dx=-dy en cosx=siny
We hebben dan: ò1/cosx dx=-ò1/siny dy =-ln(tan(1/2y)=-ln(tan(p/4-x/2))=ln(cot(p/4-x/2))=ln(tan(x/2+p/4))
(Bij de laatste twee stappen is gebruikt:
-ln(tan(p)=ln(1/tan(p))=ln(cot(p)=ln(tan(p/2-p))
De laatste vorm kan je met de goniometrische formules omzetten in
ln(1/cosx+tanx).
Succes, Lieke.
ldr
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 10 augustus 2008
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Dit is een reactie op vraag 56230
Dit is een reactie op vraag 56230