WisFaq!

Re: Re: Een deel van de oppervlakte van een cirkel

Okey hartelijk dank,

Ik wil toch wel graag weten hoe die integraal van 1/cos(x) gevonden word en ik ga de rest zelf proberen en als ik er niet uit kom dan stuur ik weer een reactie.

Met vriendelijke groet,

Bob

Bob
10-8-2008

Antwoord

Beste Bob,
Eerst even de primitieve van 1/sinx, die is nl. wat makkelijker.
Dan zullen we x vervangen door p/2-y, zodat cosx=siny.

1)Vervang sinx door 2sin(¹/₂x)cos(¹/₂x)
2)vervang x door 2y


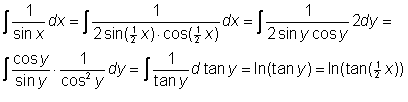
Nu ò1/cosx dx:
Nu gebruiken we de substitutie x=p/2-y (of y/2=p/4-x/2) en dus dx=-dy en cosx=siny
We hebben dan: ò1/cosx dx=-ò1/siny dy =-ln(tan(¹/₂y)=-ln(tan(p/4-x/2))=ln(cot(p/4-x/2))=ln(tan(x/2+p/4))
(Bij de laatste twee stappen is gebruikt:
-ln(tan(p)=ln(1/tan(p))=ln(cot(p)=ln(tan(p/2-p))

De laatste vorm kan je met de goniometrische formules omzetten in
ln(1/cosx+tanx).

Succes, Lieke.

ldr
10-8-2008