WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Kortste verbinding

Dit is een reactie op vraag 54424

Het is erg vervelend want ik kan in dit vak geen figuur toevoegen. Een gedeelte van mijn opdracht die ik moet doen staat op deze link. Wat ik probeerde te omschrijven is vraag 4.

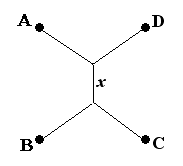
"Stel dat de situatie voor een vierkant er uitziet als hiernaast. (A, B, C en D zijn de hoekpunten van een vierkant). Bereken dan de lengte x waarvoor de totale wegenlengte minimaal is."
http://hhofstede.nl

Hopelijk kunt u mij nu nog enkele tips geven. In ieder geval alvast bedankt!
Daan M
Leerling bovenbouw havo-vwo - maandag 18 februari 2008

Antwoord

Hallo

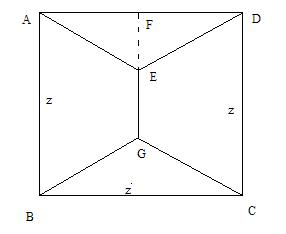
Ik veronderstel dat je uit de vorige punten van de vermelde tekst weet dat de hoek AED = 120° en dus de hoek AEF = 60° (zie tekening onderaan)
De zijde van het vierkant noemen we z
|AF| = z/2 en |EF| noemen we y
In de driehoek AEF is dan ^|AF|/_|EF| = tan(AEF) = tan(60) = Ö3

Hieruit kun je dan y berekenen en vervolgens is x = z - 2.y
Je vindt : x = z.(1-^Ö3/₃)

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 19 februari 2008