WisFaq!

Re: Kortste verbinding

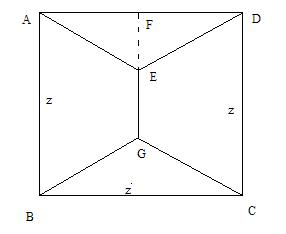
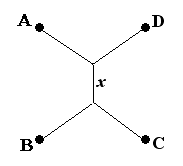
Het is erg vervelend want ik kan in dit vak geen figuur toevoegen. Een gedeelte van mijn opdracht die ik moet doen staat op deze link. Wat ik probeerde te omschrijven is vraag 4.

"Stel dat de situatie voor een vierkant er uitziet als hiernaast. (A, B, C en D zijn de hoekpunten van een vierkant). Bereken dan de lengte x waarvoor de totale wegenlengte minimaal is."
http://hhofstede.nl

Hopelijk kunt u mij nu nog enkele tips geven. In ieder geval alvast bedankt!

Daan Monster
18-2-2008

Antwoord

Hallo

Ik veronderstel dat je uit de vorige punten van de vermelde tekst weet dat de hoek AED = 120° en dus de hoek AEF = 60° (zie tekening onderaan)
De zijde van het vierkant noemen we z
|AF| = z/2 en |EF| noemen we y
In de driehoek AEF is dan ^|AF|/_|EF| = tan(AEF) = tan(60) = Ö3

Hieruit kun je dan y berekenen en vervolgens is x = z - 2.y
Je vindt : x = z.(1-^Ö3/₃)

LL
19-2-2008