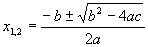|
|
|
\require{AMSmath}



Vierkantsvergelijking met parameter
kan u mij zeggen hoe ik volgende oefening oplos?
Bepaal m (E van IR)
X2-(3m +2)X +2m=0
Voorwaarde X1 groter dan 0
0 groter dan X2
hartelijk dank
lana
2de graad ASO - zaterdag 2 november 2002
Antwoord
Als je bedoeld:
x2 - (3m + 2)x + 2m = 0
Kan je m.b.v. de abcD-formule:
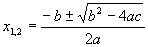
deze algemeen oplossen.
Ofwel
a = 1
b = -3m – 2
c = 2m
Invullen.
Vervolgens bepaal je in de + en de - situatie de nulpunten.
Dit zal in beide gevallen het punt m = 0 zijn.
Vervolgens bekijk je voor beide situaties twee punten, een groter dan 0, bv. 1 en een kleiner, bv. -1. En bepaal of het resultaat groter of kleiner is dan nul.
Je zult dan komen tot:
m > 0 geeft twee waarden die beide groter zijn dan 0
m < 0 geeft 1 waarde groter dan 0, en een kleiner
m = 0 geeft 0 en 1, ofwel 1 gelijk aan 0, en een groter.
Ik had dit helemaal uitgetypt, maar het zal iets teveel plaatjes opleveren. Hopelijk is dit voldoende.
M.v.g.
P.H. Stikker

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 2 november 2002
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|