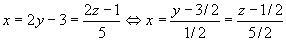WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Rechte en vlak

Dit is een reactie op vraag 43964

Ik heb nu dus gedaan:

Herschrijf het vlak in parametervorm:
a Û x=r
y=s
z=3-4r+2s

We kunnen hieruit afleiden dat V (1;0;-4) en U (0;1;2) een stel richtingsvectoren zijn van het vlak. Punt van het vlak is dan bv (0;0;3).

Stel richtingsvectoren van k?

x=0r

2y=3+0r
y= (3/2) + 0r

2z=1+5r
z=(1/2) +(5/2)r

Richtingsgetallen van k (0;0;(5/2))

Vergelijking rechte l:
l Û x=0+0r
y=0+r
z=3+2r

Scalair product met richting van k moet nul zijn

0 = ((5/2) * (3+2r))
0= 15/2 + 5r
-3/2 = r

In orde zo, of niet???

Alvast bedankt!!!
Elke
3de graad ASO - zondag 5 maart 2006

Antwoord

Beste Elke,

Van het vlak is nu alles in orde, maar je richtingsgetallen van k zijn nog altijd niet juist. Ik zie niet hoe je opeens aan die nullen komt, die coëfficiënten zijn niet 0.

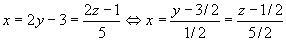
Een stel richtingsgetallen van k is dus (1,1/2,5/2).

De uiteindelijke richting van de rechte l moet een lineaire combinatie zijn van de richtingen van het vlak, zodat l in het vlak ligt. We stellen zo'n lineaire combinatie voor als richting: p(1,0,-4)+q(0,1,2)=(p,q,2q-4p).
Om p en q te bepalen neem je nu het scalair product van deze richting met de richting van k, stel dit gelijk aan 0. Eender welk koppel (p,q) dat daaraan voldoet is goed.

mvg,
Tom

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 5 maart 2006

Re: Re: Re: Rechte en vlak