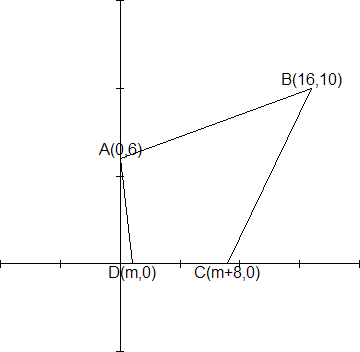|
|
|
\require{AMSmath}



Oefening op bepaalde integraal
Ik ben een student uit de 3é graad van het ASO, kunnen jullie mij op weg helpen om aan deze vraag te beginnen
Gegeven de punten A(0,6), B(16,10), C (m+8,0) en D (m,0) met m$>$0 in een orthonormaal assenstelsel, m is een parameter.
a) Teken de vierhoek ABCD
b) Bepaal de waarde van m zodat de vierhoek ABCD de kleinst mogelijke omtrek heeft. Bepaal de nulpunten zonder ICT.
Met dank,
Gerard 6EW
claes
3de graad ASO - zondag 12 december 2004
Antwoord
a)
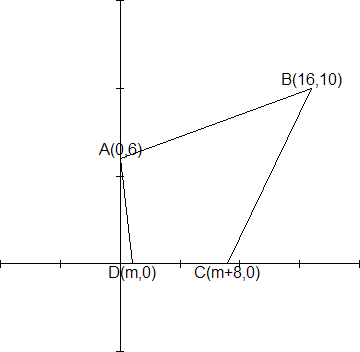
b)
De omtrek is |AB|+|BC|+|CD|+|DA| (onder |AB| versta ik de lengte van het lijnstuk AB.
|AB|=√(162+42)
|BC|=√((m+8-16)2+102)
|CD|=8
|DA|=√(m2+36)
De totale omtrek kun je nu uitdrukken in m.
Middels differentieren kun je dan de waarde(n) van m vinden waarvoor de omtrek minimaal is.
Ik zie niet in wat dit met bepaalde integralen van doen heeft!

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 12 december 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|