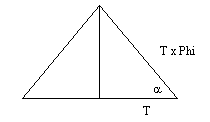|
|
|
\require{AMSmath}



Phi en piramides
Hallo, ik heb een vraag over de stelling van Pythagoras en een piramide.
Ik heb een dwarsdoorsnede van de piramide. Dus een driehoek. De hellingshoek die de schuine valkken van de piramide maken is 51.85°. Hierin is  a (rechtsonder) 51.85°. Wanneer je de schuine zijde lengte 1 geeft, dan kan je uitrekenen dat de horizontale zijde, dat is de halve breedte van de piramide, de lengte van phi heeft. Hoe kan ik dit berekenen? a (rechtsonder) 51.85°. Wanneer je de schuine zijde lengte 1 geeft, dan kan je uitrekenen dat de horizontale zijde, dat is de halve breedte van de piramide, de lengte van phi heeft. Hoe kan ik dit berekenen?
Anniek
Leerling bovenbouw havo-vwo - zaterdag 23 februari 2002
Antwoord
In een tekening ziet het er zo uit:
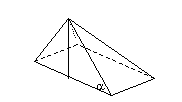 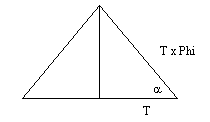
Hierin is a=51,85°. Wanneer we nu een schuine zijde lengte 1 geven, dan kun je uitrekenen dat de horizontale zijde – dat is de halve breedte van de piramide – lengte j heeft:
cos 51,85°=j/1
j=cos 51,85°=0,6177
Het is dus zo dat j 'de lengte van phi heeft'.
Zie De Grote piramide van Gizeh

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 24 februari 2002
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 a (rechtsonder) 51.85°. Wanneer je de schuine zijde lengte 1 geeft, dan kan je uitrekenen dat de horizontale zijde, dat is de halve breedte van de piramide, de lengte van phi heeft. Hoe kan ik dit berekenen?
a (rechtsonder) 51.85°. Wanneer je de schuine zijde lengte 1 geeft, dan kan je uitrekenen dat de horizontale zijde, dat is de halve breedte van de piramide, de lengte van phi heeft. Hoe kan ik dit berekenen?