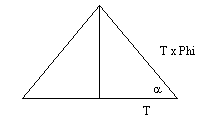WisFaq!

Phi en piramides

Hallo, ik heb een vraag over de stelling van Pythagoras en een piramide.

Ik heb een dwarsdoorsnede van de piramide. Dus een driehoek. De hellingshoek die de schuine valkken van de piramide maken is 51.85°. Hierin is a (rechtsonder) 51.85°. Wanneer je de schuine zijde lengte 1 geeft, dan kan je uitrekenen dat de horizontale zijde, dat is de halve breedte van de piramide, de lengte van phi heeft. Hoe kan ik dit berekenen?

Anniek
23-2-2002

Antwoord

In een tekening ziet het er zo uit:



Hierin is a=51,85°. Wanneer we nu een schuine zijde lengte 1 geven, dan kun je uitrekenen dat de horizontale zijde – dat is de halve breedte van de piramide – lengte j heeft:

cos 51,85°=j/1
j=cos 51,85°=0,6177

Het is dus zo dat j 'de lengte van phi heeft'.

Zie De Grote piramide van Gizeh [http://www.phys.tue.nl/TULO/guldensnede/architectuur.html]

WvR
24-2-2002