WisFaq!

Phi en de sinus van 72° en 36°

Hoe bewijs je sin(72°)/sin(36°) = $\phi$ ?

BP
29-10-2001

Antwoord

Eerst maar een driehoek tekenen met twee hoeken van 72° en een hoek van 36°.


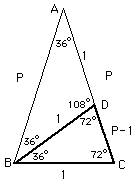
Verder heb je nodig gelijkvormigheid en de sinusregel...

Eerst zelf proberen? Lees dan niet verder...

ABCBCD (overeenkomstige hoeken zijn gelijk)
Dan geldt: BC:CD=AB:BC
Dus 1:(p-1)=p:1
Met kruislings vermenigvuldigen krijg je:
p(p-1)=1
p²-p-1=0
p=(1+√5)/2 of p=(1-√5)/2
Oh?.. aha! p=$\phi$
Dit is wel een hele bijzonder driehoek, dit is een gulden driehoek!
Wat toevallig..!

Tekenen we de driehoek nog een keer: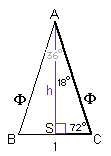

Volgens de sinusregel geldt: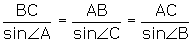



Invullen: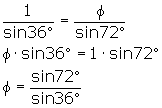

Maar misschien kan het wel veel handiger...

Zie Bron [http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/phi2DGeomTrig.html#pentag]

WvR
29-10-2001