WisFaq!

Re: Torentjes bouwen

Het bovenstaande antwoord voldoet aan de wiskundige oplossing. Alleen blijft er dan een probleem over.
Bouwer A bouwt een torentje in 36 uur, B doet dat in 45 uur. Samen hebben ze dus 2 torentjes gebouwd onafhankelijk van elkaar. Totaal aantal benodigde uren samen is volgens bovenstaande uitkomst 36 + 45 = 81 uur voor 2 torentjes onafhankelijk van elkaar.

Voor 1 torentje samen bouwen zou je dan .5 · 36 + .5 · 45 = 40.5 uur nodig hebben. Hier zit dan volgens mij het verschil in werktempo verrekend. In de vraag staat dat ze er samen 20 uur over doen om 1 toren te bouwen, dat is 40 uur in totaal. Dus voor 2 torentjes samen bouwen heb je 80 uur nodig en niet 81.

Oplossing zou dan ook kunnen zijn 35,5 uur voor A en 44,5 uur voor B. Ook hier zit 9 uur verschil tussen. Dit past alleen niet in de oplossingsvergelijking.

Ra Ra?

Groetjes van Susan en meedenkende man (Ad)

Susan Tromer
21-9-2004

Antwoord

Wat dacht je van deze redering: na 36 uur kan de eerste mee gaan bouwen aan de tweede toren. De tweede toren is dan voor 36/45-ste deel klaar. Over de resterende deel (9/45) zullen ze samen 9/45·20=4 uur doen (volgens de gegevens!).. dus nog 4 uur... in totaal kom je dan uit op 40 uur voor twee torentjes... dat is 'gemiddeld' 20 uur....

Je gaat er in je voorstel van uit dat de beide mannen samen allebei één hele toren of twee halve torens bouwen en dat is niet juist, want de eerste metselaar is gewoon sneller, dus die bouwt in dezelfde tijd 'meer toren' dan de tweede! (Tenzij de eerste na 36 uur zou gaat zitten niksen, maar dat doen we niet, daar worden ze niet voor betaald!)

Er zijn overigens heel veel leuk probleempjes waarbij het 'rekenkundig' gemiddelde geen enkele betekenis heeft.

Voorbeeld
Een automobilist rijdt van A naar B. Op de heenweg haalt de auto een gemiddelde snelheid van 80 km/uur, maar op de terugweg haalt de automobilist een gemiddelde snelheid van 100 km/uur.
Wat is de gemiddelde snelheid over de heen- terugweg samen?

Dat kan je wel berekenen! Noem de afstand van A naar B maar even d. Dan doe je over de heen weg d/80 uur en over terugweg d/100 uur. Wat is dan de gemiddelde snelheid over het hele traject?



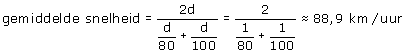
Kennelijk hangt dit 'gemiddelde' helemaal niet af van de afstand! Duidelijk is dat het in ieder geval niet 90 km/uur is. Grappig toch?

Bij de metselaars doet zich een zelfde verschijnsel voor. Dit heeft alles te maken met het Harmonisch gemiddelde. De kunst is natuurlijk om te herkennen wanneer je welk soort gemiddelde moet gebruiken, maar dat is weer een hele andere cursus...

Zie ook Als A en B een karwei kunnen klaren in 6 uur voor een variatie...

Zie Mathworld - Means [http://mathworld.wolfram.com/topics/Means.html]

WvR
22-9-2004