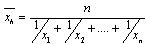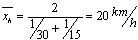WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Harmonisch gemiddelde

Wat is de definitie van het harmonisch gemiddelde? Wanneer biedt het gebruik hiervan een meerwaarde, bijv. t.o.v. het rekenkundig of een meetkundig gemiddelde?
Ton Me
Ouder - vrijdag 11 april 2003

Antwoord

Over meerwaarde wil ik eigenlijk niet praten. Er komt gewoon iets anders uit die gemiddelden, de kunst is nu om te weten in welke situatie je welk gemiddelde moet gebruiken.

Even een voorbeeldje:

Een student fietst met een hoge snelheid van 30 km/u naar zijn hogeschool om zijn examenresultaten te horen. De afstand bedraagt 15 km. De examenresultaten vallen erg tegen, waardoor hij op de terugweg met tegenzin een gemiddelde snelheid van 15km/u trapt. Bereken de gemiddelde snelheid over het hele traject.

Het normale gemiddelde zou uitkomen op (30+15)/2 = 22,5 maar klopt dat?

Laten we het probleem eens van de andere kant bekijken:
Op de heenweg heeft de student 15km gefietst in een tijd van 30 minuten (30 km/u). Op de terugweg fiets hij weer 15 km, maar dit keer doet hij er een uur over. Totaal heeft hij afgelegd 30 km in 1¹/₂ uur. Dat betekent dus een gemiddelde snelheid van 20 km/u. En dat hadden we net er niet uit gekregen.

De formule van het harmonisch gemiddelde is:

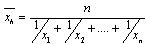
Vullen we voor het eerste traject gemiddelde snelheid 30 km/u en voor het tweede traject gemiddelde snelheid 15 km/u in, dan krijgen we:

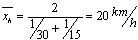
En jawel hoor dit levert wel het juiste resultaat.
Voorwaarde is wel dat de trajecten waarover de gemiddelde snelheden in de formule ingevoerd worden even groot zijn.

Een ander bekend voorbeeld van het harmonisch gemiddelde is het berekenen van het gemiddeld benzinegebruik van een auto bij het afleggen van trajecten in de stad, op de buitenweg en op de snelweg.

Met vriendelijke groet

JaDeX

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 11 april 2003