|
|
|
\require{AMSmath}




Bereken de co÷rdinaten van de keerpunten
Gegeven voor $t=0..2\pi$:
$x(t)= 4sin(t)+2sin(2t)$
$y(t)= 4cos(t)-2cos(2t)$
Bereken de co÷rdinaten van de keerpunten.
Uitwerking
Stap 1: het vinden van de $t$-waarden van de keerpunten. Dat geeft een stelsel dat je op moet lossen:
$
\begin{array}{l}
\left\{ \begin{array}{l}
\frac{{dx}}{{dt}} = 0 \\
\frac{{dy}}{{dt}} = 0 \\
\end{array} \right. \\
\left\{ \begin{array}{l}
4\cos (2t) + 4\cos (t) = 0 \\
4\sin (2t) - 4\sin (t) = 0 \\
\end{array} \right. \\
\left\{ \begin{array}{l}
\cos (2t) + \cos (t) = 0 \\
\sin (2t) - \sin (t) = 0 \\
\end{array} \right. \\
\left\{ \begin{array}{l}
2\cos ^2 (t) - 1 + \cos (t) = 0 \\
2\sin (t)\cos (t) - \sin (t) = 0 \\
\end{array} \right. \\
\left\{ \begin{array}{l}
2\cos ^2 (t) + \cos (t) - 1 = 0 \\
\sin (t)\left( {2\cos (t) - 1} \right) = 0 \\
\end{array} \right. \\
\left\{ \begin{array}{l}
(\cos (t) + 1)(2\cos (t) - 1) = 0 \\
\sin (t) = 0 \vee 2\cos (t) - 1 = 0 \\
\end{array} \right. \\
\left\{ \begin{array}{l}
\cos (t) = - 1 \vee \cos (t) = \frac{1}{2} \\
\sin (t) = 0 \vee \cos (t) = \frac{1}{2} \\
\end{array} \right. \\
\left\{ \begin{array}{l}
t = \pi + k \cdot 2\pi \vee t = \frac{1}{3}\pi + k \cdot 2\pi \vee t = 1\frac{2}{3}\pi + k \cdot 2\pi \\
t = k \cdot \pi \vee t = \frac{1}{3}\pi + k \cdot 2\pi \vee t = 1\frac{2}{3}\pi + k \cdot 2\pi \\
\end{array} \right. \\
Voor\,\,[0,2\pi ]: \\
t = \pi \vee t = \frac{1}{3}\pi \vee t = 1\frac{2}{3}\pi \\
\end{array}
$
Stap 2: vul je de gevonden waarden voor $t$ in de oorspronkelijke parametervoorstelling in om de co÷rdinaten te bepalen.
$
\begin{array}{l}
\left\{ \begin{array}{l}
x(t) = {\rm{ }}4\sin (t) + 2\sin (2t) \\
y(t) = {\rm{ }}4\cos (t) - 2\cos (2t) \\
\end{array} \right. \\
t = \pi : \\
\left\{ \begin{array}{l}
x(\pi ) = {\rm{ }}4\sin (\pi ) + 2\sin (2\pi ) = 0 \\
y(\pi ) = {\rm{ }}4\cos (\pi ) - 2\cos (2\pi ) = - 6 \\
\end{array} \right. \\
t = \frac{1}{3}\pi : \\
\left\{ \begin{array}{l}
x(\frac{1}{3}\pi ) = {\rm{ }}4\sin (\frac{1}{3}\pi ) + 2\sin (2 \cdot \frac{1}{3}\pi ) = 3\sqrt 3 \\
y(\frac{1}{3}\pi ) = {\rm{ }}4\cos (\frac{1}{3}\pi ) - 2\cos (2 \cdot \frac{1}{3}\pi ) = 3 \\
\end{array} \right. \\
t = 1\frac{2}{3}\pi : \\
\left\{ \begin{array}{l}
x(1\frac{2}{3}\pi ) = {\rm{ }}4\sin (1\frac{2}{3}\pi ) + 2\sin (2 \cdot 1\frac{2}{3}\pi ) = - 3\sqrt 3 \\
y(1\frac{2}{3}\pi ) = {\rm{ }}4\cos (1\frac{2}{3}\pi ) - 2\cos (2 \cdot 1\frac{2}{3}\pi ) = 3 \\
\end{array} \right. \\
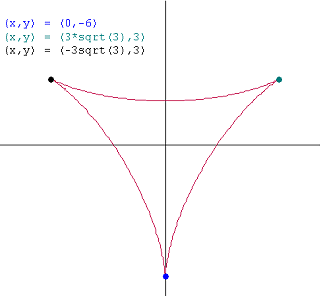
(0, - 6),\,\,(3\sqrt 3 ,3)\,\,en\,\,( - 3\sqrt 3 ,3) \\
\end{array}
$
Je hebt nu de co÷rdinaten van de keerpunten gevonden. Zo moet het kunnen...



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








