Bij de bestudering van samenhang tussen variabelen maakt men gewoonlijk onderscheid tussen variabelen die beide (min of meer) door het toeval bepaald worden (bivariaat) en variabelen waarbij er een onafhankelijke variabele en een afhankelijke variabele een rol speelt (univariaat). Bij het eerste geval wordt de samenhang aangeduidt met associatie of correlatie en in het tweede geval met regressie of variantie-analyse.
Correlatie
Je spreekt van correlatie als twee continue variabelen samenhangen of afhankelijk zijn. De uitkomsten kan je weergeven in een spreidingsdiagram. De sterkte van een (lineaire) correlatie meten we met een correlatiecoëfficiënt. Correlatie tussen twee variabelen wil nog niet zeggen, dat de verschijnselen, die door die variabelen worden gemeten, een causaal verband hebben. Soms berust het geheel op toeval en men spreekt dan wel van een schijncorrelatie.
Een klassiek voorbeeld is de correlatie tussen het aantal ooievaars en het aantal geboren kinderen. Wel een correlatie maar geen verband! De verklaring was dat er op het plattelland meer kinderen geboren worden (traditionelere levensopvatting?) en ooievaars meestal niet in de stad rond vliegen (behalve in Den Haag dan...).
Bij een 'perfecte' positieve correlatie is de correlatiecoëfficiënt r gelijk aan 1. Bij een 'perfecte' negatieve correlatie is r=-1. Als er geen correlatie is dan r=0. Dus hoe meer r afwijkt van nul hoe groter de correlatie.
Spreidingsdiagram
Hieronder zie je een voorbeeld van een spreidingsdiagram. In dat diagram kan je zien wat de samenhang is van de eindexamencijfers voor wiskunde B en natuurkunde. Elk 'stipje' stelt dus een gepaarde waarneming (de cijfers van een leerling) voor .
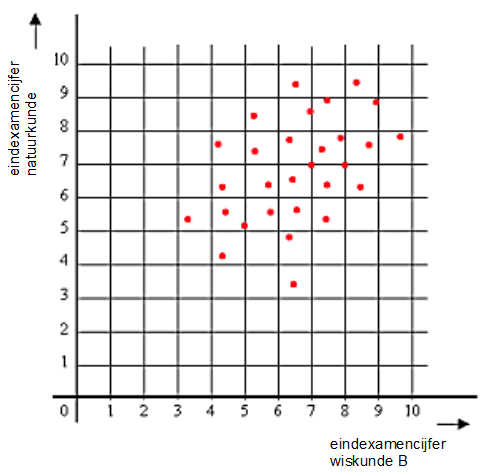
Negatieve of positieve correlatie
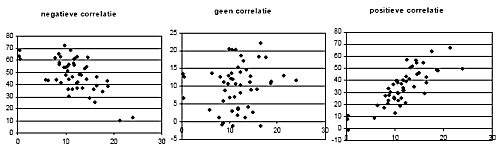
Hieronder zie je nog een paar voorbeelden, met respectievelijk een negatieve correlatie, geen correlatie en een positieve correlatie.
Voorbeeld
De resultaten van 10 studenten voor hun test (T) en hun examen (E) zijn gegeven in de onderstaande tabel:
|
T
|
10
|
12
|
8
|
13
|
9
|
10
|
7
|
14
|
11
|
6
|
|
E
|
11
|
14
|
9
|
13
|
9
|
9
|
8
|
14
|
10
|
6
|
We willen de samenhang onderzoeken en gaan een puntenwolk plotten en de correlatie berekenen met de GR.
Via onderstaande aanpak kan je het spreidingsdiagram plotten. Eerst de data in L1 en L2 zetten en dan via [STATPLOT].

Via [STAT] en Calc kies je dan voor LinReg(ax+b). Je kan dit zonder parameters doen, je GR kiest dan zelf L1 en L2, maar je kan naast de lijsten ook meteen een 'functie' opgeven waar de regressievergelijking moet worden opgeslagen. Dat kan met LinReg(ax+b)L1,L2,Y1 maar dat kan ook met LinReg(ax+b)Y1. De Y1 kan je vinden via [VARS] en dan Y-vars.

Je kunt nu een voorspelling doen over een student die op de test 12 punten haalt. Uit de tabel (via [TABLE]) kan je opmaken dat Y1=12,2.
Nu heb ik wel de regressievergelijking en de waarde van a en b maar de correlatiecoëfficiënt hebben we nog niet. Om die te krijgen moeten we de GR instellen op DiagnosticsOn. De diepere bedoeling daarvan ontgaat mij een beetje, maar dat kan je instellen via [CATALOG]. Je moet het maar weten:
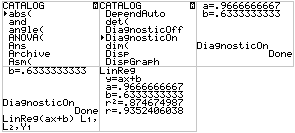
Het blijkt dat r=0,94.











