WisFaq

3. Binomiale verdeling

In het geval van n waarnemingen, alle onafhankelijk, elk resulterend in succes of mislukking, en elk met eenzelfde kans p op succes, spreekt men van een binomiale kansverdeling.

De kans op een bepaalde gebeurtenis kan men berekenen met de volgende formule:

$\eqalign{P(X=k)={n\choose{k}}\cdot p^k\cdot(1-p)^{n-k}}$

De verwachting en de standaarddeviatie kan men berekenen met:

$\mu=n\cdot{p}$ en $\sigma=\sqrt{n\cdot{p}\cdot(1-p)}$

Voorbeeld

We gooien met 10 dobbelstenen. Wat is de kans op precies 3 keer een zes?
Invullen levert:

$
\eqalign{P(X = 3) = \left( {\begin{array}{*{20}c}
{10}\\
3\\
\end{array}} \right) \cdot \left( {\frac{1}{6}} \right)^3\cdot\left({\frac{5}{6}} \right)^7 \approx 0,155}
$

Voorbeeld 2

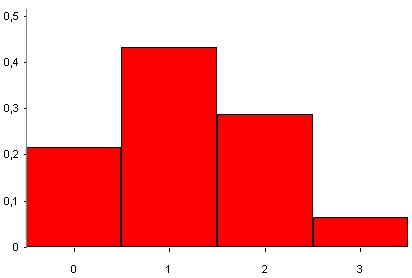
Uit een vaas met 4 rode en 6 witte knikkers worden, aselect en met teruglegging, drie knikkers getrokken. De stochast X is het aantal rode knikkers.

$\eqalign{P(X=0)={3\choose0}\cdot0,4^0\cdot0,6^3=0,216}$
$\eqalign{P(X=1)={3\choose1}\cdot0,4^1\cdot0,6^2=0,432}$
$\eqalign{P(X=2)={3\choose2}\cdot0,4^2\cdot0,6^1=0,288}$
$\eqalign{P(X=3)={3\choose3}\cdot0,4^3\cdot0,6^0=0,064}$

$E(x)=n·p=3·0,4=1,2$

Wat is de kans dat het aantal getrokken rode knikkers hoger is dan de verwachtingswaarde?

$P(X>1,2)=P(X=2)+P(X=3)=0,352$

F.A.Q.

Terug Home