1. aantal gunstige uitkomten is 8·7·6=336
   aantal mogelijke uitkomsten is 14·13·12=2184
   P(3 witte ballen)=³³⁶/₂₁₈₄=²/₁₃.

2. aantal gunstige uitkomsten is 3·8·7·6=1008
   aantal mogelijke uitkomsten is 14·13·12=2184
   P(2 witte ballen)=¹⁰⁰⁸/₂₁₈₄=⁶/₁₃.

3. aantal gunstige uitkomsten is 6·8·4·2=384
   aantal mogelijke uitkomsten is 14·13·12=2184
   P(2 witte ballen)=³⁸⁴/₂₁₈₄=¹⁶/₉₁.

4. P(minstens 2 van de zelfde kleur)=
   1-P(3 verschillende kleuren)=
   1-¹⁶/₉₁=⁷⁵/₉₁

1. 
   

   6·2·5·3 10·10·10

   =0,180

2. 
   

   _5·5·5_ 10·10·10

   =0,125

3. 
   

   _3·3·3_ 10·10·10

   =0,027

4. 
   

   P(3 wit)=

   _2·2·2_ 10·10·10

   =0,008

   0,125+0,027+0,008=0,160
5. P(minstens 1 blauw)=1-P(0 blauw)=1-(¹/₂)³=0,875

1. P(E of F)=(1000+250)/1920
2. P(F en B)=90/1920
3. P(A of E)=(1450+1000-800)/1920
4. P(-C)=(1450+280)/1920
5. Nee, er zijn er zelfs 80 studenten waarbij dat geldt.
6. Nee, je zou dan verwachten dat 'daar' 280/1920·250=36 zou staan i.p.v. 90

1. 10·10·10·10=10000
2. 10·9·8·7=5040
3. 10000-5040=4960
4. Bereken eerst hoeveel pincodes er zijn waarbij er geen cijfers na elkaar hetzelfde zijn. Dit kan op 10·9·9·9=7290 manieren. Er zijn 10000 verschillende pincodes (zie a.), dus zijn er 10000-7290=2710 mogelijkheden.

1. Er zijn twee tabellen die misschien wel handig zijn:

    

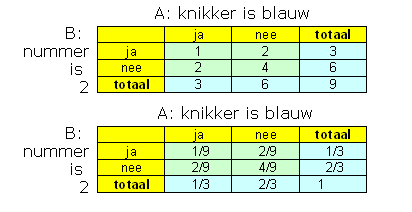
   P(A|B)=¹/₃
   (je trekt een knikker met nummer 2, wat is de kans dat ie blauw is)
   P(B|A)=¹/₃
   (je trekt een blauwe knikker, wat is de kans dat het nummer 2 is)

2. Twee manieren:
   1. Is P(A|B)=P(A) en P(B|A)=P(B)? Ja dus... (je kunt dit lezen als 'de kans op A is onafhankelijk van de vraag of B heeft plaatsgevonden'...)
   2. Is P(A en B)=P(A)·P(B)? Ja dus...

3. P(2 knikkers van dezelfde kleur)=3·³/₉·²/₈=¹/₄
   (P(rood,rood)=... er zijn 3 kleuren, dus...)

   of

   P(2 knikkers van dezelfde kleur)=1·²/₈=¹/₄
   (de eerste knikker maakt niet uit, daarna nog 2 van de 8 'goed')

   of

   Er zijn 9·8=72 verschillende manieren om 2 knikkers (zonder terugleggen) uit de vaas te pakken. Daarvan zijn er 9·2 takken die 'goed' zijn, de kans is ¹⁸/₇₂=¹/₄

4. Er twee 'verschillende' mogelijkheden... je pakt een 1 en een 3 of je pakt twee keer een 2.
   P(1,3)=³/₉·³/₈=¹/₃=¹/₈
   P(3,1) mag ook...
   ...dus P(een 1 en een 3)=¹/₄

   P(2,2)=³/₉·²/₈=¹/₁₂

   P(de som is 4)=¹/₄+¹/₁₂=¹/₃

5. P(minstens één 3)=1-P(geen 3)=1-(^6·5)/(_9·8)=1-⁵/₁₂=⁷/₁₂

1. 3!=6
2. Als 5743 de goede pincode is kan je in een boomdiagram kijken hoeveel mogelijkheden er zijn voor 2 cijfers op de goede positie:

   

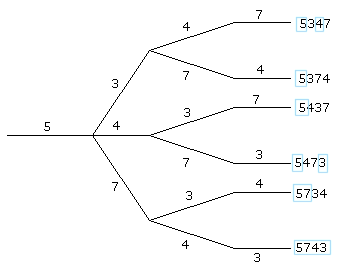
3. De kans dat het na 1 keer lukt is ¹/₆
   De kans dat het na 2 keer lukt is ⁵/₆·¹/₅
   (het is dan wel laat, maar ik ga natuurlijk niet nog een keer dezelfde pincode proberen!)
   De kans dat het na 3 keer lukt is ⁵/₆·⁴/₅·¹/₄
   Als het dan nog niet gelukt kan je het wel schudden, dus de kans is: ¹/₆+⁵/₆·¹/₅+⁵/₆·⁴/₅·¹/₄=¹/₂

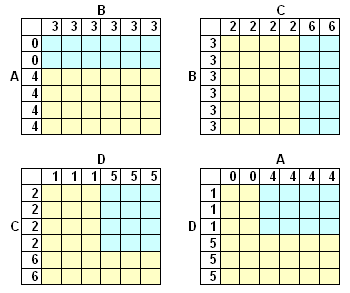
..en dat is toch verwonderlijk! Kennelijk geldt hier niet wat bij getallen geldt: a$>$b en b$>$c en a$>$c