6. Standaarddeviatie
De spreidingsmaat die het meest gebruikt wordt is de standaarddeviatie of in goed Nederlands standaardafwijking. Hierbij maken we onderscheid tussen populatiestandaardafwijking $\sigma$ en steekproefstandaardafwijking $s$. Om de standaarddeviatie (van een populatie) te berekenen neem je de volgende stappen:- Bereken het gemiddelde.
- Neem van elk getal de afstand (d) tot het gemiddelde
- Neem het kwadraat van die afstanden.
- Bereken het gemiddelde van die kwadraten.
- Neem de wortel van de uitkomst
Voorbeeld
| leeftijd in jaren | frequentie |
| 12 | 5 |
| 13 | 12 |
| 14 | 28 |
| 15 | 16 |
| 16 | 5 |
Bereken de standaarddeviatie van de leeftijden.
Uitwerking
- Het gemiddelde is (ongeveer) 14,6
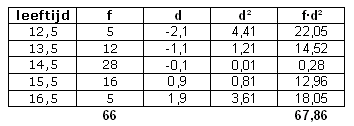
- Het gemiddelde van de kwadraten is $\large\frac{67,86}{66}\approx1,03$
- Dus de standaarddeviatie is $\sqrt{1,03}\approx1,01$
Formules
De formule voor de standaarddeviatie van een populatie ziet er dan zo uit:
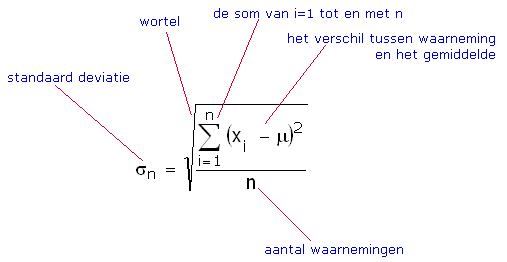
De formule voor de standaarddeviatie van een steekproef ziet er dan zo uit:
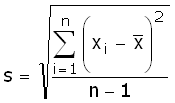
Oefening
Bereken de standaarddeviatie van de volgende twee steekproeven.- Steekproef A: 11, 22, 53, 64, 85 en 96
- Steekproef B: 1, 50, 51, 52, 53 en 86
Antwoorden
|
Steekproef A: $\overline x\approx55,2$ $s\approx33,7$ |
Steekproef B: $\overline x\approx48,8$ $s\approx27,2$ |
F.A.Q.