7. Een voorbeeld
In de tabel hier kun je de leeftijden vinden van een groep mensen.
| leeftijd | frequentie |
| 0-5 | 3 |
| 6-11 | 8 |
| 12-17 | 9 |
| 18-23 | 5 |
- Bereken het gemiddelde en de standaarddeviatie
- Bepaal m.b.v. een somfrequentiepolygoon de mediaan, q1 en q3
- Teken het boxplot
Uitwerking
a
Om het gemiddelde en de standaarddeviatie te berekenen heb je van elke klasse het klassemidden nodig. Je gaat er van uit dat het gemiddelde van elke klasse het klassemidden is.
Je krijgt de volgende tabel:
| leeftijd | frequentie |
| 3 | 3 |
| 9 | 8 |
| 15 | 9 |
| 21 | 5 |
Het gaat hier over leeftijd, dus de klasse 0-5 zijn alle nul tot vijfjarigen. Dus de linker klassegrens is 0 en de rechter klassegrens is 6. Het klassemidden van de eerste klasse is 3. Met behulp van een tabel (of een rekenmachine) kun je nu het gemiddelde en standaarddeviatie bepalen. Het gemiddelde is 12,8 en de standaarddeviatie is 5,6.
b
Voor het tekenen van een somfrequentiepolygoon bereken je eerst de cumulatieve frequentie.
| leeftijd | freq. | cumu- latieve freq. |
| 3 | 3 | 3 |
| 9 | 8 | 11 |
| 15 | 9 | 20 |
| 21 | 5 | 25 |
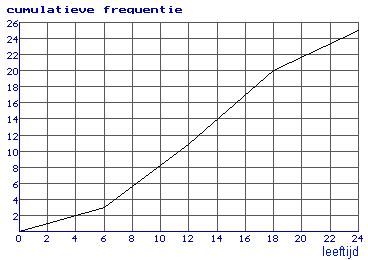
Bij het tekenen van de somfrequentiepolygoon gebruik je horizontaal een schaalverdeling en de rechter klassengrens. Je krijgt dan de tekening rechtsboven.
De mediaan is de leeftijd waarbij 50% van de leeftijden lager en 50% van de leeftijden hoger is. Je kunt de mediaan aflezen bij 12,5.
q1 en q3 kun je op dezelfde manier aflezen bij 6,25 resp. 18,75.
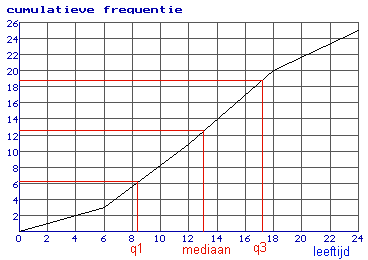
De mediaan is 13, q1=8,4 en q3=17,2
c
In een boxplot moet je de kleinste waarde, q1, mediaan, q3 en de grootste waarde af kunnen lezen.
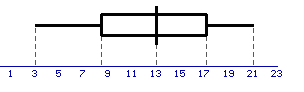
Hierboven zie je de boxplot. We nemen als kleinste waarde 3 (zie tabel) en als grootste waarde 21. Of zou het beter zijn als kleinste waarde 0 en als grootste waarde 24 te nemen ?