6. Standaarddeviatie
De spreidingsmaat die het meest gebruikt wordt is de standaarddeviatie of in goed Nederlands standaardafwijking. Hierbij maken we onderscheid tussen populatiestandaardafwijking \sigma en steekproefstandaardafwijking s. Om de standaarddeviatie (van een populatie) te berekenen neem je de volgende stappen:- Bereken het gemiddelde.
- Neem van elk getal de afstand (d) tot het gemiddelde
- Neem het kwadraat van die afstanden.
- Bereken het gemiddelde van die kwadraten.
- Neem de wortel van de uitkomst
Voorbeeld
| leeftijd in jaren | frequentie |
| 12 | 5 |
| 13 | 12 |
| 14 | 28 |
| 15 | 16 |
| 16 | 5 |
Bereken de standaarddeviatie van de leeftijden.
Uitwerking
- Het gemiddelde is (ongeveer) 14,6
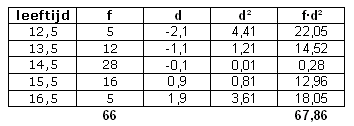
- Het gemiddelde van de kwadraten is \large\frac{67,86}{66}\approx1,03
- Dus de standaarddeviatie is \sqrt{1,03}\approx1,01
Formules
De formule voor de standaarddeviatie van een populatie ziet er dan zo uit:
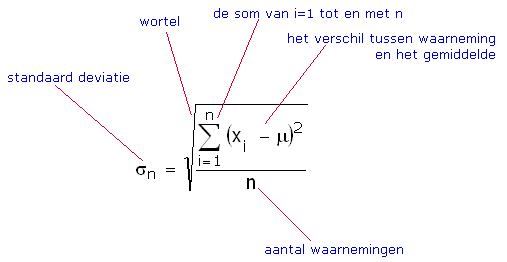
De formule voor de standaarddeviatie van een steekproef ziet er dan zo uit:
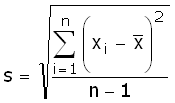
Oefening
Bereken de standaarddeviatie van de volgende twee steekproeven.- Steekproef A: 11, 22, 53, 64, 85 en 96
- Steekproef B: 1, 50, 51, 52, 53 en 86
Antwoorden
|
Steekproef A: \overline x\approx55,2 s\approx33,7 |
Steekproef B: \overline x\approx48,8 s\approx27,2 |
F.A.Q.