Volgens Wikipedia:
In de analyse is een buigpunt van een kromme een punt op de kromme waar de kromming van teken verandert. De vorm van de kromme verandert van hol in bol of omgekeerd.
Bij functies kan je de buigpunten vinden door te kijken naar de tweede afgeleide.
Hoe zit dat?
Bij een functie kan in een buigpunt afnemende stijging over gaan in toenemende stijging. Je ziet hier een voorbeeld van:
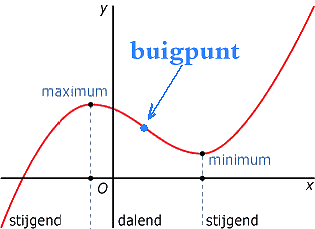
Je kunt ook zeggen dat de afname een minumum bereikt. Dat betekent dat de afgeleide een minimum heeft. Hoe kan je van de afgeleide extremen vinden? Door te kijken naar de afgeleide van de afgeleide. Dat noemen we dan de tweede afgeleide.
Hieronder zie je een voorbeeld van de grafiek van een functie, de afgeleide en de tweede afgeleide:
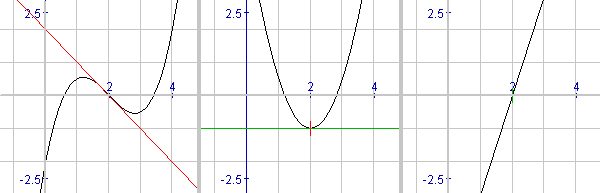
Voor een buigpunt geldt in ieder geval dat f''(x)=0. Dit is echter nog geen voldoende voorwaarde. Je moet dan nog laten zien dat de tweede afgeleide van teken wisselt.
F.A.Q.

