5. Kwartielafstand

De kwartielafstand is een spreidingsmaat. De kwartielafstand is het verschil tussen het derde en het eerste kwartiel.

De mediaan verdeelt de gegevens in twee evengrote stukken: 50% eronder en 50% erboven. Je kunt op deze manier een hoeveelheid gegevens ook in vieren verdelen. Dus in 4 stukken van elk 25% van de gegevens. De grenzen van deze vier gebieden worden kwartielen genoemd: q₁, q₂ en q₃. Uiteraard is q₂ hetzelfde als de mediaan.
De afstand van q₁ en q₃ is een maat voor spreiding.

Je kunt q₁ ook opvatten als de mediaan van de onderste helft en q₃ als mediaan van de bovenste helft. Het bepalen van q₁ en q₃ lijkt erg veel op het bepalen van de mediaan.
Dus ook hier maak je onderscheid tussen discrete en continue variabelen.

Voorbeeld

Al je te maken hebt met een continue variabele kun je voor het bepalen van de kwartielafstand gebruik maken van een somfrequentiepolygoon. Hieronder zie je zo'n somfrequentiepolygoon met relatieve frequenties. Om de kwartielafstand te bepalen kun je q₁ en q₃ uit de grafiek af lezen.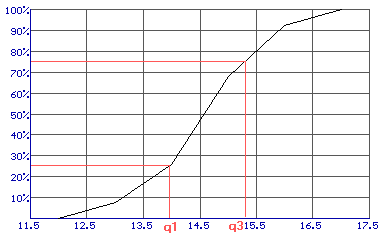



q₁=14,0 en q₃=15,3.
De kwartielafstand is dan q₃ - q₁ = 15,3 - 14,0 = 1,3.

Nog een voorbeeld:

Hieronder zie een steelbladdiagram van proefwerkcijfers van een klas. Omdat je hier over alle gegevens beschikt kun je om de kwartielen te bepalen 'gewoon' gaan tellen.
Links staan de gegevens van de meisjes, rechts die van de jongens.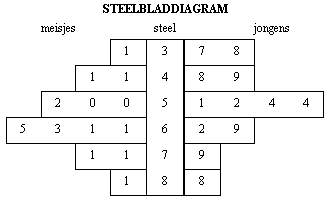



Je kunt op de volgende manier de kwartielafstand bepalen:

Meisjes:

• Bepaal de mediaan. De mediaan is 6,1
• Bepaal de onderste helft. De onderste helft is nummer 1 tot en met nummer 7.
• Bepaal de mediaan van de onderste helft. De mediaan van de onderste helft is 5,0
• Bepaal de bovenste helft. De bovenste helft is nummer 7 tot en met nummer 13.
• Bepaal de mediaan van de bovenste helft. De mediaan van de bovenste helft is 6,5
• De kwartielafstand is 6,5 - 5,0 = 1,5

Jongens:

• Bepaal de mediaan. De mediaan is 5,3
• Bepaal de onderste helft. De onderste helft is nummer 1 tot en met nummer 6.
• Bepaal de mediaan van de onderste helft. De mediaan van de onderste helft is 4,85
• Bepaal de bovenste helft. De bovenste helft is nummer 7 tot en met nummer 12.
• Bepaal de mediaan van de bovenste helft. De mediaan van de bovenste helft is 6,55
• De kwartielafstand is 6,55 - 4,85 = 1,6

Oefening

Bepaal de kwartielafstand van de hele klas.
Antwoord: de kwartielafstand is 1,6

Tip

Hoe kan je nu handig de mediaan en de kwartielen bepalen?

A.
Neem aan: je hebt 25 gegevens, #1^t/_m#25 Neem (1+25)/2=13 het 13^de getal is de mediaan.

B.
Neem aan: je het 26 gegevens, #1^t/_m#26 Neem (1+26)/2=13,5 neem het gemiddelde van het 13^de en het 14^de gegeven.

In het geval B neem je als eerste kwartiel de 'mediaan' van de onderste helft. Dat zijn de nummers 1^t/_m13 Op dezelfde manier als boven... (1+13)/2=7 dus het 7^de gegeven is het eerste kwartiel. Zo ook voor het derde kwartiel... 14^t/_m26 Neem (14+26)/2=20 Het 20^ste gegeven is het derde kwartiel. So far so good....

Maar... in het geval A heb je een 'probleem'. Wat is de onderste en wat is de bovenste helft?

I.
Neem je 1^t/_m12 als onderste helft en 14^t/_m25 als bovenste helft? En laat je de mediaan (dat is toch de middelste) buiten beschouwing.

II.
Of neem je 1^t/_m13 als onderste helft en 13^t/_m25 als bovenste helft? En laat je de mediaan gewoon 2 keer 'meedoen'.

Als je kiest voor I. dan is het eerste kwartiel het gemiddelde van het 6^de en 7^de gegeven en in geval II. is het eerste kwartiel het 7^de gegeven. Dit kan tot twee verschillende uitkomsten leiden... in schoolboeken kan je beide 'manieren' tegenkomen.

Welke manier is nu beter? Tja... wie het weet mag het zeggen. Op zich is het van weinig belang. Je gebruikt de kwartielafstand (bijvoorbeeld) niet als een 'absoluut' gegeven maar om verschillende gegevens met elkaar te vergelijken... en als je dan maar 'consequent' blijft lijkt me er weinig aan de hand.

F.A.Q.

• Kwartielafstand

©2004-2024 WisFaq