WisFaq!

Als het (bijvoorbeeld) gaat om een voetbalwedstrijd en er wordt 12 keer gescoord dan zijn er verschillende scoreverlopen denkbaar.

Neem aan dat A en B tegen elkaar spelen. Voor elk doelpunt kan je dan kiezen uit 'A scoort' of 'B scoort'. Je kunt dan gebruik maken van een roosterdiagram. In dit geval moet je voor elk doelpunt kiezen tussen A of B.

Dat geeft dan $
2^{12} = 4096
$ mogelijke scoreverlopen!

Hopelijk geeft dat een antwoord op je vraag. Zo niet dan nog maar even doorvragen!

Helpt dat?
WvR
28-2-2024

Hoeveel combinaties zijn er mogelijk?

Ik heb een schilderij die bestaat uit 15 vlakken, opgesteld in een matrix van 5 bij 3. Per rij van 5 is dat dus 120 maal 3 en per kolom 6 maal 3. Maar hoe moet je dan berekenen hoeveel combinatiemogelijkheden je hebt over de hele matrix?
Ivan
30-3-2024

Antwoord

Als je $15$ vlakken hebt en daar de getallen $1$ tot en met $15$ in wilt plaatsen kom je op $15!$ uit, ofwel
$$
1\times2\times3\times4\times5\times6\times7\times8\times9\times10\times11\times12\times13\times14\times15
$$
Of had je andere invullingen in gedachten?
kphart
31-3-2024

Anagrammen van LOKAAL

Anagrammen van LOKAAL
Telproblemen in voorbeelden

Roger
14-4-2024

Antwoord

Er zijn 6! woorden te maken met 6 letters, maar omdat de A’s onderling verwisselbaar zijn moet je nog delen door 2 en wegens de verwisselbaarheid van de L-en deel je nog een keer door 2. Je komt dan uit op 180 verschillende anagrammen.
Helpt dat?
WvR
14-4-2024

Getallen van vier cijfers met minsten één zes

U is de verzameling van alle natuurlijke getallen met vier cijfers. Geen enkel getal begint met nul. Hoeveel van die getallen bevatten minstens één zes?
Mimi
1-5-2024

Antwoord

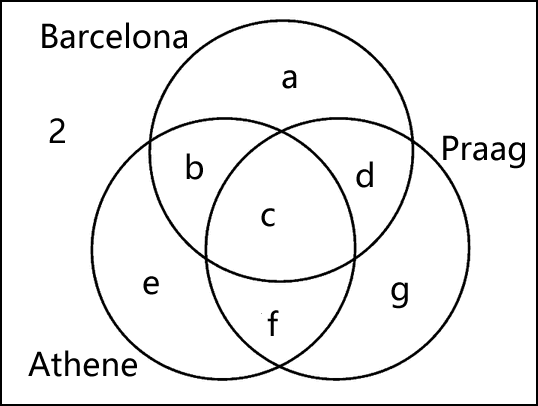
Er zijn 9·10·10·10=9000 getallen van 4 cijfers waarbij geen enkel getal met 0 begint. De vraag is nu hoeveel getallen met minstens één zes zijn daar bij?

Het is handig om te kijken hoeveel getallen er dan zijn zonder een zes. Dat zijn 8·9·9·9=5832 getallen .

Dus…?

Helpt dat?😀
WvR
1-5-2024

Barcelona, Praag of Athene

Ik heb moeilijkheden met volgende vraag: Er werd door 110 leerlingen gestemd welke van de drie steden (Barcelona, Praag of Athene) geschikt zijn als bestemmingen voor hun schoolreis. Hierbij kom op meerdere steden gestemd worden.

Athene kreeg 60 stemmen, Barcelona 63 stemmen en Praag 57 stemmen.

- 31 leerlingen stemden zowel op Athene als Barcelona.
- 25 leerlingen stemden zowel op Barcelona als Praag.
- 33 leerlingen stemden zowel op Athene als Praag.
- 2 leerlingen onthielden zich van de stemming.

Ik begrijp niet zo goed hoe ik dit in een venndiagram kan plaatsen.
Eline
9-6-2024

Antwoord

Ik zou een Venn-diagram tekenen met daarin de verschillende gebeieden. Je krijgt dan:

Je kunt dan 7 vergelijkingen opstellen met 7 onbekenden. Dat zou (in principe) oplosbaar kunnen zijn. Je krijgt dan:

b + c + e + f = 60
a + b + c + d = 63
c + d + f + g = 57
b + c = 31
c + d = 25
c + f = 33
a + b + c + d + e + f + g + 2 = 110

Je kunt 's proberen het stelsel op te lossen. Wat is handig? Hoe pak je dat aan? Zou dat lukken?
WvR
9-6-2024

Gooien met drie dobbelstenen

Hoeveel mogelijkheid zijn er om met drie gewone dobbelstenen in totaal
a. 17 ogen te gooien
B. 16 ogen te gooien
C. Minstens 16 ogen te gooien
D. 6 ogen te gooien
Otto
20-11-2024

Antwoord

Hallo Otto,

Zoals je in de spelregels kunt lezen, is het niet de bedoeling dat je 'zomaar' een vraag stelt in de hoop dat wij deze voor je oplossen. Laat op zijn minst weten waar het probleem zit, of wat je zelf hebt geprobeerd. Dan kunnen we je helpen om de stof beter te begrijpen.

Ik ga ervan uit dat je niet weet hoe je de vraag moet aanpakken. Daarom geef ik je enkele hints om je op weg te helpen. Lukt het daarmee nog niet, stel dan gerust een vervolgvraag, dan helpen we je verder.

Vraag b)
Ga eerst na met welke combinaties van ogen je 16 kunt gooien. Dit kan door:
twee zessen te gooien en één vier, of
één zes en twee vijven.
Voor beide mogelijkheden geldt dat er 3 volgordes zijn (voor twee zessen en één vier zijn dit 664, 646 en 466). In totaal zijn er dus 2 $\times $ 3=6 mogelijkheden om 16 ogen te gooien.

Vraag a)
Dezelfde aanpak als vraag b. Je vindt hier minder mogelijkheden.

Vraag c)
Vragen met 'minstens', 'meer dan', 'niet minder dan' splits je eerst in 'precies $<$ dit $>$ of precies $<$ dat $>$ of precies .....'
In dit geval: minstens 16 betekent 'precies 16 of precies 17 of precies 18' (meer dan 18 is met drie dobbelstenen niet mogelijk). Bereken voor elk van deze drie aantallen het aantal mogelijkheden en tel deze bij elkaar op.

Vraag d)
Dezelfde aanpak als vraag a) en b).

Lukt het hiermee?
GHvD
21-11-2024