|
|
|
\require{AMSmath}
Praktische opdrachten
Re: Afstandsbepaling op de aardbol
Dag Oscar, wij moeten voor school hetzelfde doen als hier. Alleen snappen we niet goed hoe het werkt. We denken dat we het juist doen maar de uitkomst klopt niet. We doen dit voor Santiago in Chili tot Sydney. Kan je ons hierbij helpen. Alvast bedankt
Jan-Wi
22-1-2024
Antwoord

Hallo Jan-Willem,
Jammer dat je jouw berekeningen niet vermeldt, anders hadden we kunnen meedenken over waar jouw fouten dan zitten. Ik geef aan hoe je de berekening kunt uitvoeren volgens de methode van de vraag waarop je reageert.
Santiago en Sidney liggen (nagenoeg) op dezelfde breedtecirkel: afgekapt op hele graden is dit 33°. De straal r van deze breedtecirkel kan je berekenen door de aarde te bekijken vanaf een punt boven de evenaar, zie de figuur hieronder:
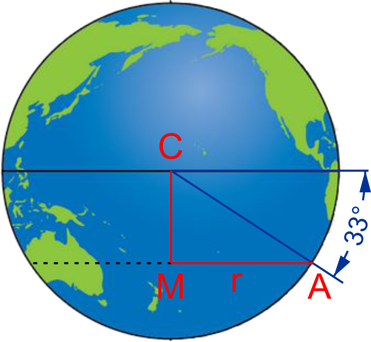
AC is de straal van de aarde, hoek A in driehoek AMC is de breedtegraad 33°, hiermee is de straal r van deze breedtegraad te berekenen.
Laten we dan de aarde eens bekijken vanaf een punt boven de zuidpool:
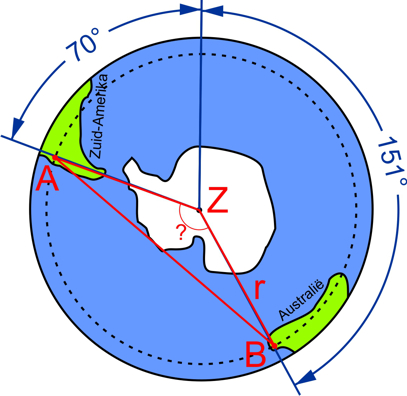
Z is de zuidpool, punt A geeft de ligging van Santiago aan, punt B de ligging van Sydney. De lengtegraden zijn ook aangegeven: 70° WL resp. 151° OL. Hiermee is hoek Z in driehoek AZB te berekenen. Omdat je de zijden ZA en ZB kent (de straal r van de breedtecirkel) kan je ook lijnstuk AB berekenen: de afstand tussen Santiago en Sydney, gemeten langs een rechte lijn dwars door de aarde heen.
Tot slot kijken we vanuit het middelpunt C van de aarde naar de punten A en B:
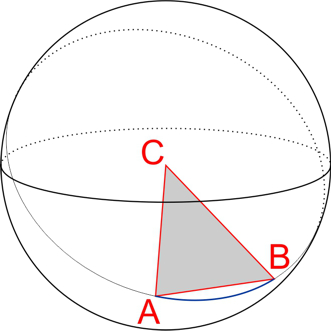
Van de driehoek ABC ken je alle zijden, dus je kunt hoek C berekenen. Wanneer je hoek C eenmaal hebt, bereken je de booglengte AB door te bedenken dat deze hoek C een deel van 360° is, de booglengte AB is datzelfde deel van de omtrek van de aarde.
Lukt het hiermee? Zo niet, stel dan gerust een vervolgvraag, maar geef dan wel aan waar het probleem ligt.
Overigens: het vraagstuk is ook op te lossen met behulp van boldriehoeksmeetkunde, kijk maar eens op Hoever is het van ... naar ...?
GHvD
23-1-2024
Afstandsbepaling op aardebol
ik moet een onderzoek doen over afstandsbepaling op aardebol. ik moet in een opdracht de afstand tussen Gibraltar en Tokyo berekenen. ik weet dat voor het berekenen van de afstand tussen twee steden die op dezelfde breedtegraad liggen moet men eerst de straal bepalen van de overeenkomstige breedtecirkel. Tokio en Gibraltar liggen allebei op 36°NB. ik had deze afstand eerst berekend adhv de cosinusregel, maar blijkbaar is er ook een andere manier om dat te doen. zou u mij kunnen helpen
joke
8-3-2024
Antwoord

Hallo Joke,
Kijk eens bij Re: Afstandsbepaling op de aardbol en Hoever is het van ... naar ...?, daar vind je informatie over hoe je deze vraag kunt aanpakken.
GHvD
8-3-2024
Spelschema
Ik moet een spelschema maken dat voldoet aan de volgende eisen:- 10 teams
- 5 spellen
- teams speelt maximaal 2 keer hetzelfde spel
- alle spellen worden gespeelt met 1 team tegen 1 ander team
- uiteindelijk moet ieder team 1 keer tegen allen andere 9 teams gespeeld hebben.
Wie kan een speelschema voor mij maken dat hieraan voldoet?
Gillis
9-6-2024
Antwoord

Hallo Gillis,
Je zou het als volgt kunnen aanpakken:
Teken een 10-hoek, en zet bij de hoekpunten de letters A t/m J, zie de figuur hieronder. Deze stellen de 10 teams voor. Verbind letters horizontaal met 5 gekleurde horizontale lijnen. De 5 kleuren stellen de spellen voor. In de linker figuur zie je dat in de eerste ronde de teams A en B tegen elkaar spelen met het rode spel, teams C en J spelen tegen elkaar met het gele spel enz.:
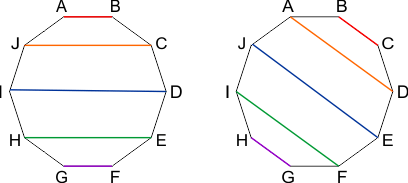
Voor de tweede ronde draai je de gekleurde lijnen naar een volgende speler, zo krijg je de rechter figuur. Nu spelen teams B en C het rode spel, teams D en J het gele spel enz. Op deze wijze kan je de eerste 5 ronden samenstellen. Verder draaien heeft geen zin, want dan zouden teams A en B opnieuw tegen elkaar spelen (met het paarse spel), en dat is niet toegestaan.
Daarom starten we deze procedure opnieuw voor een 2e fase, met een andere verbinding tussen teams, zie de linker figuur hieronder:
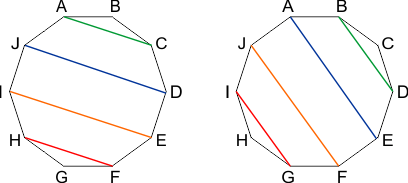
Teams A en C starten met het groene spel, teams D en J met blauw enz. De teams B en G hebben een rustmoment. Draai de gekleurde lijnen weer om de teams voor de volgende ronde te selecteren. Na vier keer spelen in deze 2e fase heb je negen ronden gehad en heeft elk team tegen elk ander team gepeeld.
Voor het verdelen van de spellen komt wel wat hand-puzzelwerk kijken: in deze 2e fase worden in elke ronde maar 4 van de 5 spellen gespeeld, steeds is dus één spel buiten bedrijf. Laat bij elke ronde een ander spel buiten bedrijf. Hiermee lukte het mij na enig proberen om ervoor te zorgen dat elke speler hooguit 2 keer hetzelfde spel speelt. Lukt het jou ook?
GHvD
11-6-2024



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|












