WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Limieten

Limiet bepalen van meerdere veranderlijken

Beste

In de bijlage staat de oefening waar ik moeilijkheden mee heb. Ik heb tot nu toe al veel waarden aan y toegekend, zoals y- $>$ kx, y- $>$ x², y- $>$ 1/x en ik kom allemaal als limiet 0 uit. Ik ben er dus van uit dat het limiet bestaat, aangezien ze overal hetzelfde is. Maar ik weet niet direct hoe ik dat moet bewijzen. Bijvoorbeeld de formule L(x,y)=f(a,b)+f/x(a,b)(x−a)+f/y(a,b)(y−b) gebruiken met (a,b) waarden die dicht bij 0 zitten (bv. (0.1, 0.1). Maar ik weet niet of dit als geldig "bewijs" wordt gezien. Kan u mij hiermij opweg helpen? (zie bijlage)
Alvast bedankt.
Jacob
4-1-2024

Antwoord

Als $x=0$ dan hebben we $f(0,y)=0$.
Als $x\neq0$ kunnen we afschatten:
$$
\frac{x^2y^2}{x^2+y^4}\le\frac{x^2y^2}{x^2}=y^2
$$
en dat is goed genoeg.
kphart
4-1-2024

Limiet van een onbepaaldheid

Ik heb een opgave gekregen over een limiet die een onbepaaldheid uitkomt (oneindig delen door oneindig). De teller bestaat uit 3 tot de n-de macht plus 200 en de noemer bestaat uit 3 tot de n-1ste macht min 2. Ik heb geprobeerd de breuk op de splitsen in 4 termen, maar dan kom ik nog steeds onbepaaldheden uit.
Lena M
14-1-2024

Antwoord

Je kunt teller en noemer delen door $3^{n-1}$. Je krijgt dan:

$
\eqalign{\mathop {\lim }\limits_{n \to \infty } \frac{{3^n + 200}}
{{3^{n - 1} - 2}} = \mathop {\lim }\limits_{n \to \infty } \frac{{3 + \frac{{200}}
{{3^{n - 1} }}}}
{{1 - \frac{2}
{{3^{n - 1} }}}} = 3 }
$

Helpt dat?
WvR
14-1-2024

Limiet recursieve functie

f(n) is gedefinieerd als volgt: voor n=0 geld f(n) = 1, anders is f(n) gelijk aan f(n-1)+¹/_f(n-1), nu is mijn vraag: 'Convergeert deze functie? Zo ja, wat is lim_{n $\to $ $\infty $}(f(n)) dan?'

Heel erg bedankt voor uw hulp!
Oliver
24-3-2024

Antwoord

Merk allereerst op dat de rij stijgend is:
$$f(n)=f(n-1)+\frac1{f(n-1)} > f(n-1)
$$Teken de webgrafiek van de getallenrij die je zo krijgt:

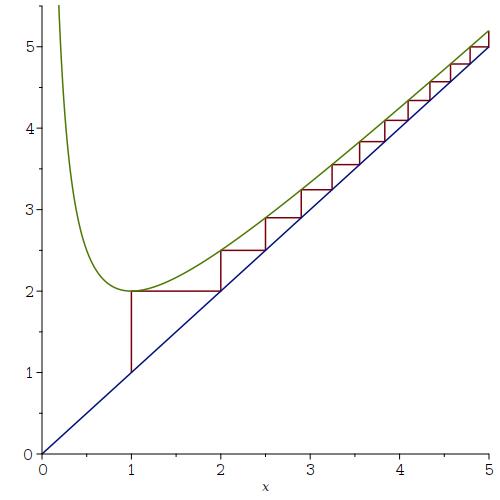
Dat suggereert dat de waarden onbeperkt toenemen, en dat de rij divergeert.

Inderdaad: als de rij zou convergeren naar $L$ dan zou $L$ aan de vergelijking $L=L+\frac1L$ moeten voldoen, maar die heeft geen oplossing, dus $\dots$
kphart
24-3-2024

Re: Limiet recursieve functie

Bedankt voor uw snelle antwoord op mijn vraag!
Ik heb echter nog een vraag: 'Welk programma hebt u gebruikt om deze grafiek te creëren?' Het zou heel handig zijn als ik dit ook zou kunnen gebruiken zodat ik zelf makkelijk grafieken zoals deze kan maken. Alvast bedankt voor uw antwoord!
Oliver
7-6-2024

Antwoord

Ik heb Maple gebruikt, maar die is duur (onze universiteit heeft een licensie).
Je kunt het met Geogebra, dat programma wordt veel in het voortgezet onderwijs gebruikt en gebruikers hebben al veel dingen voorgeprogrammeerd, kijk hier maar eens.
kphart
7-6-2024

Limiet naar oneindig

Beste

Kan iemand me helpen met onderstaande oefening?
Veronderstel dat p en q vaste reële getallen zijn met p $<$ −1 $<$ q $<$ 0 en dat L = lim n→+∞ (1-qn)/(p-qn)

Welke uitspraak is dan waar?

(A) L $<$ −1
(B) −1 $<$ L $<$ 0
(C) 0 $<$ L $<$ 1
(D) 1 $<$ L

Alvast bedankt.
Caro
25-6-2024

Antwoord

Bedoel je
$$\lim_{n\to\infty}\frac{1-qn}{p-qn}\qquad
\text{ of }\qquad
\lim_{n\to\infty}\frac{1-q^n}{p-q^n}
$$Ik vermoed de tweede want
$$\lim_{n\to\infty}\frac{1-qn}{p-qn}=\lim_{n\to\infty}\frac{\frac1n-q}{\frac pn-q}=1
$$en dat staat niet bij de mogelijkheden.

Voor de tweede geldt
$$\lim_{n\to\infty}\frac{1-q^n}{p-q^n}=\frac{1-0}{p-0}=\frac1p
$$Welk alternatief geeft dat?

kphart
25-6-2024

Re: Limiet naar oneindig

Ik zie dat ik een typefoutje heb gemaakt. Het moest zijn: L = lim n→+∞ (1-qn)/(q-pn). Als ik de methode gebruik zoals in uw eerste situatie, dan kom ik C uit. Heel erg bedankt!
Caro
25-6-2024

Antwoord

Prima.
Voor de andere lezers, de limiet is dan gelijk aan $\frac qp$.
kphart
25-6-2024