
Integreren van de wortel van een functie tot de derde macht
Beste Wisfaqmannen/vrouwen,
Ik doe een avondcursus HBO-Industriele automatisering. Mijn vooropleiding is MTS dus de wiskunde vind ik pittig. Ik ben al een tijdje bezig met het volgende vraagstukje:
ò[6x/{x^2+x+1)^(3/2)}]dx
met de aanwijzing X+1/2=1/2Ö3tg(Y)
Ik heb al het een en ander uitgewerkt maar kom nu echt niet meer verder.
X+1/2=1/2Ö3tgY
tanY=(x+1/2)/(1/2Ö3)
Y=arctan(x+1/2)/(1/2Ö3)
en
x^2+x+1=(x+1/2)^2+3/4
(1/2Ö3tgY)^2+3/4
tan^2Y+3/4=3/4(tan^2Y+1)
tan^2+1=(sin^2Y/cos^2Y)+1=1/cos^2Y
3/4(1/cos^2Y)
Û(x^2+x+1)^(3/2)=(3/4*(1/cos^2Y))^(3/2)
(3/4^(3/2))*(1/((cos^2Y)^(3/2))
(3/4^(3/2))*(1/(cos^3Y))
1/((X^2+x+1)^(3/2))=(cos^3Y)/(3/4^(3/2))
dat resulteert dus in de integraal:
ò(6*x*cos^3Y)/(3/4^(3/2))dx
En vanaf hier kom ik maar niet verder. Als ik partieel wil integreren dan zit ik met die Y. Wat moet ik daarmee doen?
Ik snap er steeds minder van lijkt het wel.
Mark
Student hbo - zaterdag 6 januari 2007
Antwoord
Beste Mark,
Een eerste opmerking: in je laatste integraal komt zowel Y als x voor, dat is niet goed. Wanneer je een substitutie doet moet je alles omzetten in de nieuwe veranderlijke, ook de 'dx' bijvoorbeeld.
De substitutie die als aanwijzing gegeven wordt is goed, maar komt misschien wat 'uit de lucht gevallen'. Ik zal eerst tonen waarom die logisch is. In de noemer kan je een volkomen kwadraat vormen ('kwadraat afsplitsen'):
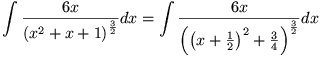
Nu hebben we in de noemer iets van de vorm f(x)2+a2 met a = Ö(3/4) = Ö3/2. Daarvoor is de substitutie f(x) = a.tan(y) ideaal (ik neem voor het gemak y in plaats van Y). In ons geval is f(x) = x+1/2, dus de substitutie is x + 1/2 = Ö3/2 tan(y).
Zoals ik al zei moeten we alles wat in de integraal in x staat, nu schrijven in functie van y. We hebben nog een '6x' en een 'dx'. Uit de substitutie volgt ook direct dat:
x = Ö3/2 tan(y) -1/2 Þ dx = Ö3/2 1/cos2(y) dy
In de laatste stap heb ik beide leden gedifferentieerd om dx te schrijven in functie van dy. Nu vervangen we alles in x door de gevonden uitdrukkingen in y:
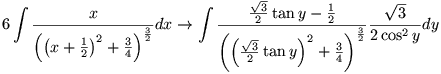
Dit ziet er misschien nog erger uit dan de oorspronkelijke integraal, maar je kan nu veel vereenvoudigen. In de noemer gaat die substitutie handig zijn om gebruik te maken van 1+tan2a = 1/cos2a en dan kan je verder vereenvoudigen.
mvg,
Tom

zondag 7 januari 2007
 ©2001-2024 WisFaq
©2001-2024 WisFaq
|