
Vergelijking van cirkels door snijpunten van cirkels
Ik moet vergelijkingen berekenen van de cirkels die door de snijpunten van x2+y2+2x+6y-7=0 en x2+y2-1=0 gaan en bovendien raken aan y=x. Hoe doe ik dit?
charlo
Student hbo - vrijdag 15 augustus 2003
Antwoord
De algemene vergelijking van een cirkel: x2+y2+2ax+2by+c=0
Je zoekt eerst de snijpunten van die twee vergelijkingen door het stelsel
x2+y2+2x+6y-7=0
x2+y2-1=0
op te lossen.
Dit stelsel heeft 2 oplossingen. nl (0,1) en (3/5,4/5)
Deze punten moeten voldoen aan de vergelijking van de cirkel. Dus:
1+2b+c=0
en
(3/5)2 + (4/5)2 + a 6/5 + b 8/5 + c=0
of dus:
0·a +2·b+c=-1
6/5·a+8/5·b+c = -1
Dit stelsel los je op met de methode van gauss jordan. Je krijgt eventueel als oplossing (het kan ook een andere zijn, afhankelijk van de keuze van de parameter):
a = t
b = 3 t
c = -1 - 6 t
Dit geeft een stelsel van 3 onbekenden en twee vergelijkingen. Dus 1 vrijheidsgraad (parameter t). Om die weg te werken is er een derde voorwaarde. Dat is dat de cirkel moet raken aan y=x.
Wat we tot nu toe hebben is dat alle cirkels van de vorm
x2+y2+2ax+2by+c=0
met a = t, b = 3 t en c = -1 - 6 t
in aanmerking komen. Dus de cirkel is van de vorm
x2+y2+2·t·x+6·t·y-1-6·t = 0
Het feit dat y=x hieraan moet raken wil zeggen dat als je de snijpunten zoekt, je er maar één mag vinden. Terwijl een gewone rechte en een cirkel meestal twee of geen gemeenschappelijke punten heeft.
Dus het stelsel
x2+y2+2·t·x+6·t·y-1-6·t = 0
y=x
Mag slechts één oplossing hebben.
Dus vervang y door x:
2·x2+8·t·x-1-6·t = 0
Dit is een verkantsvergelijking. Bereken de discriminant en stel hem nul, want dat is de voorwaarde voor 1 oplossing.
discr=(8·t)2-4·2·(-1-6·t) =0
Dis is opnieuw een tweedegraadsvergelijking in t die twee oplossingen heeft:
{t = -1/4}, {t = -1/2}
Als we deze waarden in de vergelijking van de cirkel stoppen krijgen we dus twee cirkels, nl:
X2+Y2-X-3·Y+2 = 0
en
X2+Y2-1/2·X-3/2·Y+1/2 = 0
Een figuurtje:
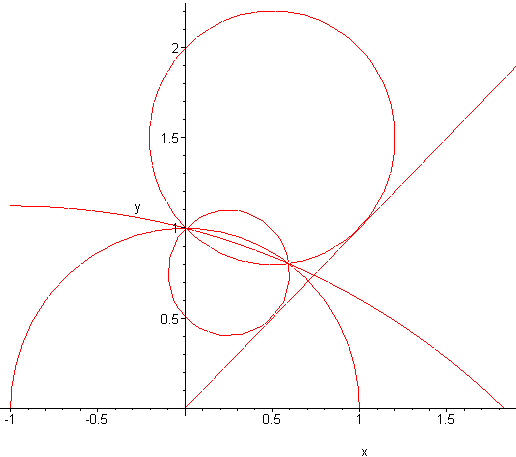
Veel plezier er nog mee.
Koen Mahieu

vrijdag 15 augustus 2003
 ©2001-2024 WisFaq
©2001-2024 WisFaq
|