\require{AMSmath}

Re: Cosinus niet in eenheidscirkel

Dit is een reactie op vraag 98362

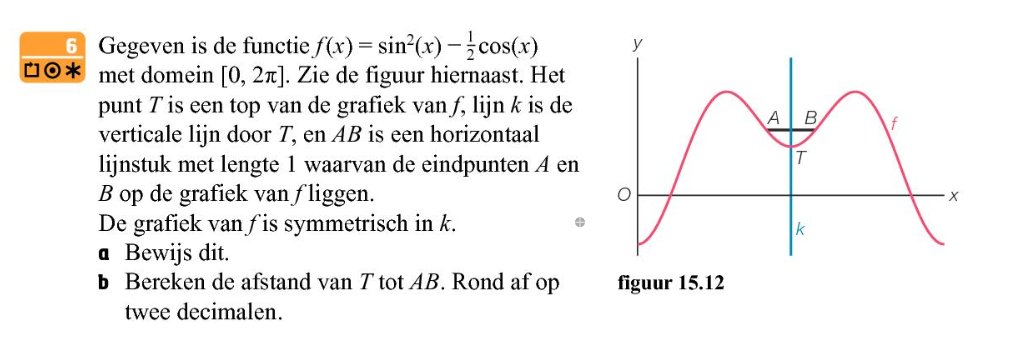
Opgave in bijlage.

Leerling bovenbouw havo-vwo - dinsdag 29 oktober 2024

Antwoord

Ik heb de uitwerking hier ingeplakt:

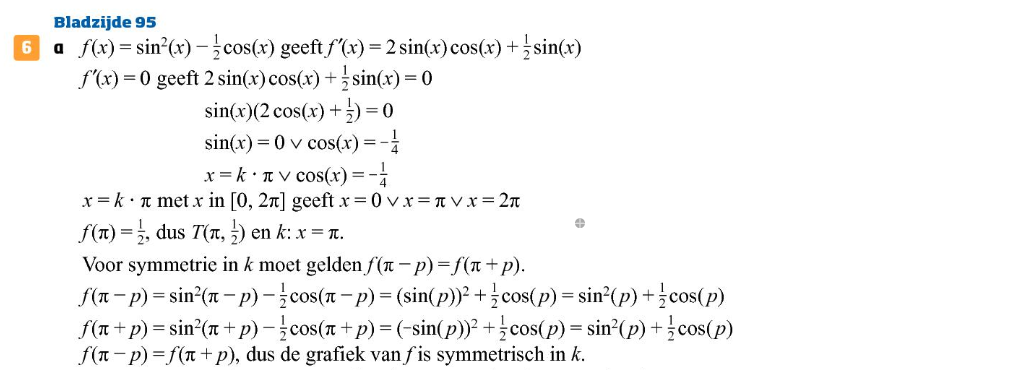
Die uitwerking verdient niet de schoonheidsprijs (de som ook niet vind ik). Er zou op zijn minst uitgelegd moeten worden waarom het geval $\cos(x)=-\frac14$ terzijde wordt gelegd. En ook vertelt men niet waarom $\pi$ de juiste waarde is, en ook niet waarom er bij $\pi$ een top ligt.

Je zou ook als volgt kunnen redeneren: als de functie symmetrisch ten opzichte van $k$ is moet $k$ wel door $(\pi,0)$ (het midden van het interval $[0,2\pi]$) gaan.
(Ik denk dat dat ook de gedachte achter de uitwerking in het boek is: kijken of $\pi$ bij de $x$-en zit met $f'(x)=0; maar dat kun je ook doen door gewoon invullen.)
Dus ik bewijs dat $f$ symmetrisch is ten opzichte van $\pi$ en dat $f$ voor $x=\pi$ een top heeft.

Het eerste is makkelijk als je bedenkt dat $\cos(\pi+x)=\cos(-(\pi+x))=\cos(-(\pi+x)+2\pi)=\cos(\pi-x)$, en ook dat $\sin^2(x)=1-\cos^2(x)$. Dan komt er
$$
f(\pi+x)=1-\cos^2(\pi+x)-\frac12\cos(\pi+x)=1-\cos^2(\pi-x)-\frac12\cos(\pi-x)=f(\pi-x)
$$
Het tweede ook: $f'(x)=2\sin(x)\cdot\cos(x)+\frac12\sin(x)=\sin(2x)+\frac12\sin(x)$, dus $f'(\pi)=0$; verder geldt $f''(x)=2\cos(2x)+\frac12\cos(x)$, dus $f''(\pi)=\frac32$ en dat is positief, dus bij $\pi$ zit een lokaal minimum.

Overigens kun je voor de punten waar $\cos(x)=-\frac14$ geldt op deze manier laten zien dat daar een lokaal maximum zit want je kunt $f''(x)$ schrijven als $4\cos^2(x)-2+\frac12\cos(x)$, dan heb je $x$ niet nodig want je kunt meteen $-\frac14$ voor elke $\cos(x)$ invullen. Het resultaat is $-\frac{15}8$ en dat is negatief.

©2004-2024 WisFaq