\require{AMSmath}

Lengte van stalen assen

In een fabriek maakt men stalen assen. de lengte van de assen is normaal verdeeld. de standaardafwijking in de lengte van de assen is 0,2 m. Deze standaardafwijking kan worden verkleind door een grotere nauwkeurigheid vd zaagmachine in te stellen. an het einde vd productielijn worden assen waarvan een lengte meer dan 0,4 mm verschilt verwijderd.

Hoe groot moet de standaarafwijking zijn als er slechts 1% uitval mag zijn?

anne z
Leerling bovenbouw havo-vwo - maandag 16 december 2002

Antwoord

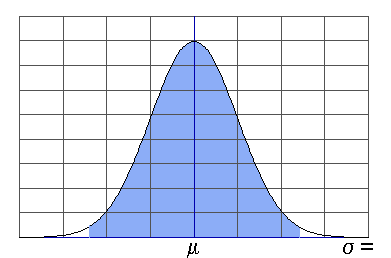
Op de 'oude manier' zou je denken dat je je deze opgave zo zou kunnen oplossen:



x=100,4
$\phi$(z)=0,99 $\Rightarrow$ z=2,576
$\mu$=100 (zullen we maar even zeggen)
en $\sigma$ wil ik graag weten.

Je zou dan eerst bepalen wat de z-waarde is die hoort bij $\phi$(z)=0,99 (tweezijdig) en dan kan je met deze formule uitrekenen wat $\sigma$ zou moeten zijn:



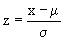
En dan vervolgens:



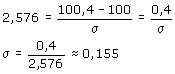
..en als ik het me goed herinner had jij dit ook!?

Met de rekenmachine zou ik met:
Y1=normalcdf(0.4,100,0,x)
Y2=0,005
en window=[0,1]x[0,0.1] en dan calc/intersect hetzelfde moeten krijgen...? Alleen had ik voor het gemiddelde 100 genomen in plaats van 0, maar het idee is hetzelfde.

Dus hier wordt het gebied uitgerekend rechts van 0,4 (tot veel) bij een gemiddelde van 0 en de standaarddeviatie wordt zo gekozen dat het gebied dan 0,005 wordt.

Hopelijk is het duidelijk, anders horen we het wel.

WvR
maandag 16 december 2002

©2001-2024 WisFaq