De standaardafwijking berekenen met de rekenmachine

ik heb de gegevens 551 mm is het gemiddelde van een buis, bij een bepaalde soort is het nodig dat ze een minimale lengte hebben van 548,6 2,3% moet vernietigd worden.
op mijn uitwerkingen staat:
P9X$<$548,6/$\mu$=551 en $\sigma$=$\sigma$₀ = 0,023
dus p(z, 548,6-551/$\sigma$₀ = 0,0230
P(Z$<$-1.9953)=0.0230
en $\sigma$₀ = 0.0230

Maar wat moet ik intikken en waar om die $\sigma$0 te krijgen?

Lonnek
Leerling bovenbouw havo-vwo - zondag 11 januari 2004

Antwoord

Op je uitwerking staat iets als:

$
\eqalign{
& P(X < 548,6) = 0,023 \cr
& \Phi (z) = 0,023 \cr
& z = - 1,9954 \cr
& \frac{{548,6 - 551}}
{\sigma } = - 1,9954 \cr
& \sigma = \frac{{548,6 - 551}}
{{ - 1,9954}} \approx 1,20 \cr}
$

Allemaal waar natuurlijk, maar gebruik je de standaardnormale verdeling eigenlijk wel? Misschien wel niet...

Zie eventueel Normale verdeling voor meer uitleg en voorbeelden. Of vraag nog even!

Maar kennelijk wil je het met je GR doen! Dat kan ook:
Gegevens:
$\mu$=551
P(X$\leq$548,6)=0,023
Gevraagd: wat is $\sigma$?

Ik ga er even vanuit dat je een Ti83 hebt.
Type bij y= de volgende 'functie' in:

Y1=normalcdf(-1E99,548.6,551,X)

Ik wil met deze functie een X vinden zodat Y1=0.023, dus zet ik deze er ook nog in:

Y2=0.023

Nu moet ik wel even bij WINDOW een geschikt scherm kiezen. Kies X bijvoorbeeld van 0 tot 3 (even experimenteren!). Zet Y in ieder geval van [0,0.03].

Teken de grafiek en bereken met CALC en INTERSECT het snijpunt van Y1 en Y2.



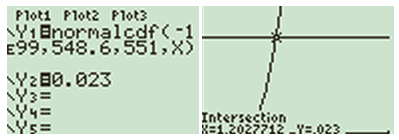
Je vindt dan dat $\sigma\approx$1.203 Ik zelf zou gewoon de staardnormale verdeling gebruiken, maar och... zo kan het ook.

Een ander manier is de volgende (ik geef je alleen de schermpjes):



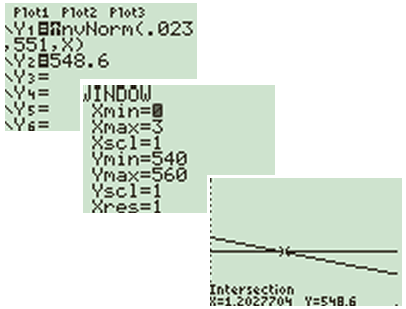
Kortom, eenvoudig is het niet, maar eenmaal begrepen zou het moeten kunnen.

Vragen naar aanleiding van dit antwoord? Klik rechts..! zondag 11 januari 2004

©2004-2024 WisFaq