WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Integraal over S1

Beste

Ik probeer om in te zien als jij een 1-vorm w op S¹ integreert, dat de waarde van de integraal niet verandert indien we 1 punt excluderen bv. S¹\{1}. Ik dacht om f₁=1 op S¹\{1} en 0 in een omgeving van 1 bv. B(1,1/n) en analoog f₂=0 op S¹\{1} en 1 in B(1,1/n). Zodat f₁+f₂=1, of als we nu $\smallint $ w= $\smallint $ (f₁+f₂)w= $\smallint $ f₁w+ $\smallint $ f₂w. De integraal van f₁w is precies de integraal van w op S1\{1}. En voor de 2de integraal dacht ik als n- $>$ inf dan krijgen we de integraal van w op {1} wat 0 moet zijn omdat w een 1 vorm is en {1} 0-dimensionaal. Is deze redenering correct? Alvast bedankt!
Rafik
Student universiteit België - zaterdag 25 maart 2023

Antwoord

Het klinkt redelijk. Maar er zijn wat verbeterpunten: je $f_1$ en $f_2$ hangen van $n$ af en de integraal van $f_1\cdot w$ is bij zo'n vaste $n$ niet automatisch gelijk aan de integraal van $w$. Bij de tweede integraal doe je het wel goed: een limiet nemen.

Verder kun je niet tegelijk $f_1$ gelijk aan $1$ nemen op $S^1\setminus\{1\}$ èn gelijk aan $0$ op een omgeving van $1$. Idem voor $f_2$.

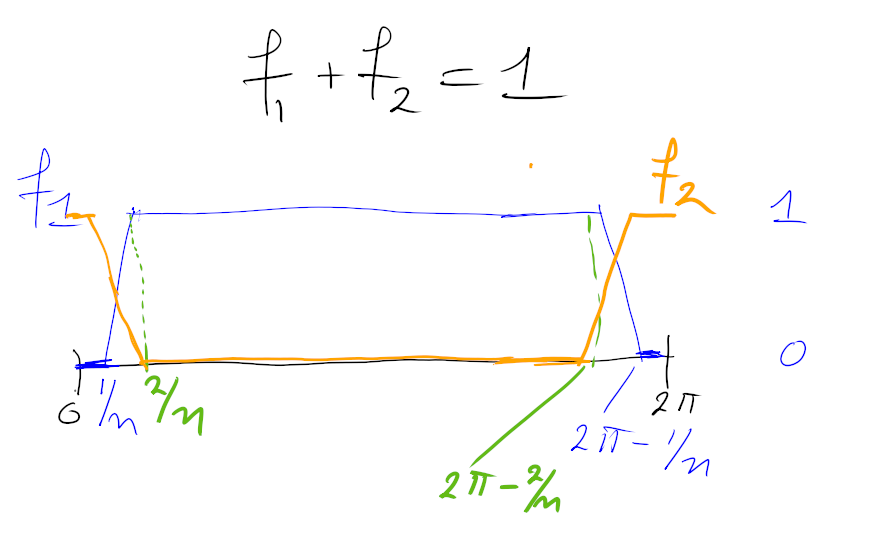
In het plaatje zie je twee functies die je naar $S_1$ kun verplaatsen via een parametrizering ($x(t)=(\cos(t),\sin(t))$).
Die zou je dan $f_{1,n}$ en $f_{2,n}$ moeten noemen.
Nu kun je de limieten nemen
$$
\lim_{n\to\infty}\int f_{1,n}w \text{ en } \lim_{n\to\infty}\int f_{1,n}w
$$

kphart

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 5 april 2023